题目内容
已知椭圆C1: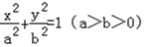 的离心率为
的离心率为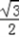 ,一个焦点坐标为
,一个焦点坐标为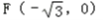 .
.
(1)求椭圆C1的方程;
(2)点N是椭圆的左顶点,点P是椭圆C1上不同于点N的任意一点,连接NP并延长交椭圆右准线与点T,求 的取值范围;
的取值范围;
(3)设曲线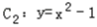 与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当
与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当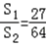 时,求直线AB的方程.
时,求直线AB的方程.
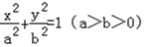 的离心率为
的离心率为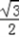 ,一个焦点坐标为
,一个焦点坐标为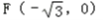 .
.(1)求椭圆C1的方程;
(2)点N是椭圆的左顶点,点P是椭圆C1上不同于点N的任意一点,连接NP并延长交椭圆右准线与点T,求
 的取值范围;
的取值范围;(3)设曲线
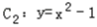 与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当
与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当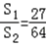 时,求直线AB的方程.
时,求直线AB的方程.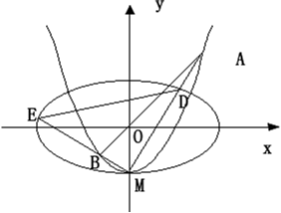
解:(1)∵椭圆C1: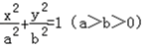 的离心率为
的离心率为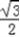 ,
,
一个焦点坐标为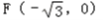 ,
,
∴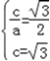 ,∴a=2,c=
,∴a=2,c= ,b=
,b=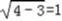 ,
,
∴椭圆C1的方程为: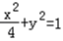 .
.
(2)∵N是椭圆C1: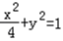 的左顶点,点P是椭圆C1上不同于点N的任意一点,
的左顶点,点P是椭圆C1上不同于点N的任意一点,
∴N(﹣2,0),椭圆右准线:x=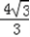 ,
,
设P(x,y),则 =
=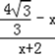 ,
,
∵﹣2≤x≤2,∴ =
=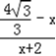 ∈[
∈[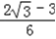 ,+∞).
,+∞).
故 的取值范围是[
的取值范围是[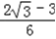 ,+∞).
,+∞).
(3)设直线MA的斜率为k1,则直线MA的方程为y=k1x﹣1.
由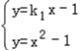 ,解得
,解得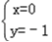 ,或
,或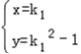 .
.
则点A的坐标为(k1,k12﹣1).
又直线MB的斜率为﹣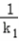 ,同理可得点B的坐标为(﹣
,同理可得点B的坐标为(﹣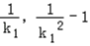 ).
).
于是S1= |MA||MB|=
|MA||MB|=
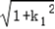 |k1|
|k1|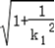 |﹣
|﹣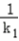 |=
|=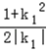 .
.
由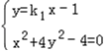 ,得(1+4k12)x2﹣8k1x=0.
,得(1+4k12)x2﹣8k1x=0.
解得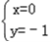 ,或
,或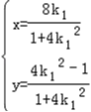 ,
,
则点D的坐标为(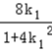 ,
,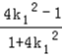 ).
).
又直线ME的斜率为﹣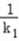 .
.
同理可得点E的坐标为(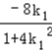 ,
, ).
).
于是S2= |MD||ME|=
|MD||ME|=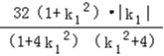 .
.
故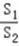 =
=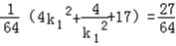 ,
,
解得k12=2,或k12= .
.
又由点A,B的坐标得,k=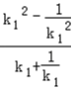 =k1﹣
=k1﹣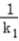 .
.
所以k=±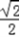 .
.
故满足条件的直线存在,且有两条,
其方程为y=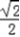 x和y=﹣
x和y=﹣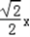 .
.
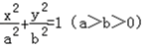 的离心率为
的离心率为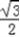 ,
,一个焦点坐标为
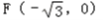 ,
,∴
 ,∴a=2,c=
,∴a=2,c= ,b=
,b=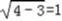 ,
,∴椭圆C1的方程为:
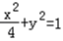 .
.(2)∵N是椭圆C1:
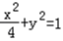 的左顶点,点P是椭圆C1上不同于点N的任意一点,
的左顶点,点P是椭圆C1上不同于点N的任意一点,∴N(﹣2,0),椭圆右准线:x=
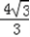 ,
,设P(x,y),则
 =
=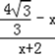 ,
,∵﹣2≤x≤2,∴
 =
=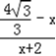 ∈[
∈[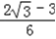 ,+∞).
,+∞).故
 的取值范围是[
的取值范围是[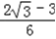 ,+∞).
,+∞).(3)设直线MA的斜率为k1,则直线MA的方程为y=k1x﹣1.
由
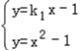 ,解得
,解得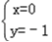 ,或
,或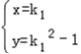 .
.则点A的坐标为(k1,k12﹣1).
又直线MB的斜率为﹣
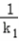 ,同理可得点B的坐标为(﹣
,同理可得点B的坐标为(﹣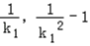 ).
).于是S1=
 |MA||MB|=
|MA||MB|=
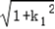 |k1|
|k1|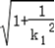 |﹣
|﹣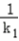 |=
|=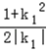 .
.由
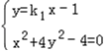 ,得(1+4k12)x2﹣8k1x=0.
,得(1+4k12)x2﹣8k1x=0.解得
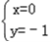 ,或
,或 ,
,则点D的坐标为(
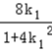 ,
,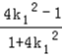 ).
).又直线ME的斜率为﹣
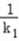 .
.同理可得点E的坐标为(
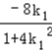 ,
, ).
).于是S2=
 |MD||ME|=
|MD||ME|=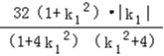 .
.故
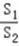 =
=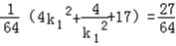 ,
,解得k12=2,或k12=
 .
.又由点A,B的坐标得,k=
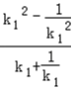 =k1﹣
=k1﹣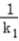 .
.所以k=±
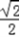 .
.故满足条件的直线存在,且有两条,
其方程为y=
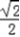 x和y=﹣
x和y=﹣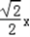 .
.
练习册系列答案
相关题目
 的离心率为
的离心率为 ,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.
,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切. 的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切,
,直线l:y=x+2与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切,  的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。  的离心率为
的离心率为 ,一个焦点坐标为
,一个焦点坐标为 .
. 的取值范围;
的取值范围; 与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、
与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、 时,求直线AB的方程.
时,求直线AB的方程.
 的离心率为e,且b,e,
的离心率为e,且b,e, 为等比数列,曲线y=8-x2恰好过椭圆的焦点.
为等比数列,曲线y=8-x2恰好过椭圆的焦点. 的顶点和焦点分别是椭圆C1的焦点和顶点,设O为坐标原点,点A,B分别是C1和C2上的点,问是否存在A,B满足
的顶点和焦点分别是椭圆C1的焦点和顶点,设O为坐标原点,点A,B分别是C1和C2上的点,问是否存在A,B满足 .请说明理由.若存在,请求出直线AB的方程.
.请说明理由.若存在,请求出直线AB的方程.