题目内容
已知椭圆C1: 的离心率为
的离心率为 ,一个焦点坐标为
,一个焦点坐标为 .
.(1)求椭圆C1的方程;
(2)点N是椭圆的左顶点,点P是椭圆C1上不同于点N的任意一点,连接
NP并延长交椭圆右准线与点T,求
 的取值范围;
的取值范围;(3)设曲线
 与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、
与y轴的交点为M,过M作两条互相垂直的直线与曲线C2、椭圆C1相交于点A、D和B、E,(如图),记△MAB、△MDE的面积分别是S1,S2,当
 时,求直线AB的方程.
时,求直线AB的方程.
【答案】分析:(1)先利用离心率和焦点坐标,得到一个关于参数的方程组,解这个方程组即可求出参数,进而求出椭圆C1的方程.
(2)由题设条件行求出N(-2,0),椭圆右准线:x= ,设P(x,y),则
,设P(x,y),则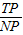 =
= ,再由-2≤x≤2,能求出
,再由-2≤x≤2,能求出 的取值范围.
的取值范围.
(3)先把直线MA的方程与抛物线方程联立可得点A的坐标,再利用弦长公式求出|MA|,同样的方法求出|MB|进而求出S1,同理可求S2.再代入已知就可知道是否存在直线l满足题中条件了.
解答:解:(1)∵椭圆C1: 的离心率为
的离心率为 ,
,
一个焦点坐标为 ,
,
∴ ,
,
∴a=2,c= ,b=
,b= ,
,
∴椭圆C1的方程为: .
.
(2)∵N是椭圆C1: 的左顶点,点P是椭圆C1上不同于点N的任意一点,
的左顶点,点P是椭圆C1上不同于点N的任意一点,
∴N(-2,0),椭圆右准线:x=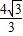 ,
,
设P(x,y),则 =
= ,
,
∵-2≤x≤2,
∴ =
= ∈[
∈[ ,+∞).
,+∞).
故 的取值范围是[
的取值范围是[ ,+∞).
,+∞).
(3)设直线MA的斜率为k1,则直线MA的方程为y=k1x-1.
由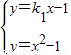 ,解得
,解得 ,或
,或 .
.
则点A的坐标为(k1,k12-1).
又直线MB的斜率为- ,同理可得点B的坐标为(-
,同理可得点B的坐标为(- ).
).
于是S1= |MA|•|MB|=
|MA|•|MB|=
 •|k1|•
•|k1|• •|-
•|- |=
|= .
.
由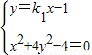 ,得(1+4k12)x2-8k1x=0.
,得(1+4k12)x2-8k1x=0.
解得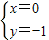 ,或
,或 ,则点D的坐标为(
,则点D的坐标为( ,
, ).
).
又直线ME的斜率为- .同理可得点E的坐标为(
.同理可得点E的坐标为( ,
, ).
).
于是S2= |MD|•|ME|=
|MD|•|ME|=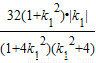 .
.
故 =
= ,解得k12=2,或k12=
,解得k12=2,或k12= .
.
又由点A,B的坐标得,k= =k1-
=k1- .所以k=±
.所以k=± .
.
故满足条件的直线存在,且有两条,其方程为y= x和y=-
x和y=- .
.
点评:本题是对椭圆与抛物线以及直线与抛物线和直线与椭圆的综合问题的考查.是一道整理过程很麻烦的题,需要要认真,细致的态度才能把题目作好.
(2)由题设条件行求出N(-2,0),椭圆右准线:x=
 ,设P(x,y),则
,设P(x,y),则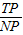 =
= ,再由-2≤x≤2,能求出
,再由-2≤x≤2,能求出 的取值范围.
的取值范围.(3)先把直线MA的方程与抛物线方程联立可得点A的坐标,再利用弦长公式求出|MA|,同样的方法求出|MB|进而求出S1,同理可求S2.再代入已知就可知道是否存在直线l满足题中条件了.
解答:解:(1)∵椭圆C1:
 的离心率为
的离心率为 ,
,一个焦点坐标为
 ,
,∴
 ,
,∴a=2,c=
 ,b=
,b= ,
,∴椭圆C1的方程为:
 .
.(2)∵N是椭圆C1:
 的左顶点,点P是椭圆C1上不同于点N的任意一点,
的左顶点,点P是椭圆C1上不同于点N的任意一点,∴N(-2,0),椭圆右准线:x=
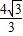 ,
,设P(x,y),则
 =
= ,
,∵-2≤x≤2,
∴
 =
= ∈[
∈[ ,+∞).
,+∞).故
 的取值范围是[
的取值范围是[ ,+∞).
,+∞).(3)设直线MA的斜率为k1,则直线MA的方程为y=k1x-1.
由
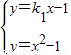 ,解得
,解得 ,或
,或 .
.则点A的坐标为(k1,k12-1).
又直线MB的斜率为-
 ,同理可得点B的坐标为(-
,同理可得点B的坐标为(- ).
).于是S1=
 |MA|•|MB|=
|MA|•|MB|=
 •|k1|•
•|k1|• •|-
•|- |=
|= .
.由
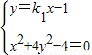 ,得(1+4k12)x2-8k1x=0.
,得(1+4k12)x2-8k1x=0.解得
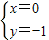 ,或
,或 ,则点D的坐标为(
,则点D的坐标为( ,
, ).
).又直线ME的斜率为-
 .同理可得点E的坐标为(
.同理可得点E的坐标为( ,
, ).
).于是S2=
 |MD|•|ME|=
|MD|•|ME|=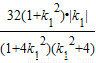 .
.故
 =
= ,解得k12=2,或k12=
,解得k12=2,或k12= .
.又由点A,B的坐标得,k=
 =k1-
=k1- .所以k=±
.所以k=± .
.故满足条件的直线存在,且有两条,其方程为y=
 x和y=-
x和y=- .
.点评:本题是对椭圆与抛物线以及直线与抛物线和直线与椭圆的综合问题的考查.是一道整理过程很麻烦的题,需要要认真,细致的态度才能把题目作好.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.
,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切. 的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切,
,直线l:y=x+2与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切,  的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。  的离心率为e,且b,e,
的离心率为e,且b,e, 为等比数列,曲线y=8-x2恰好过椭圆的焦点.
为等比数列,曲线y=8-x2恰好过椭圆的焦点. 的顶点和焦点分别是椭圆C1的焦点和顶点,设O为坐标原点,点A,B分别是C1和C2上的点,问是否存在A,B满足
的顶点和焦点分别是椭圆C1的焦点和顶点,设O为坐标原点,点A,B分别是C1和C2上的点,问是否存在A,B满足 .请说明理由.若存在,请求出直线AB的方程.
.请说明理由.若存在,请求出直线AB的方程.