题目内容
(本小题满分12分)在等比数列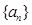 中,
中,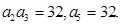
(1)求数列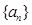 的通项公式;
的通项公式;
(2)设数列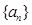 的前
的前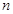 项和为
项和为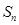 ,求
,求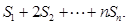
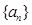 中,
中,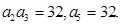
(1)求数列
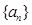 的通项公式;
的通项公式;(2)设数列
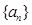 的前
的前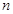 项和为
项和为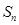 ,求
,求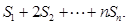
解:(Ⅰ)设等比数列{an}的公比为q,依题意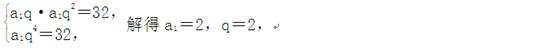 ∴an=2·2n-1=2n. …4分
∴an=2·2n-1=2n. …4分
(Ⅱ)Sn=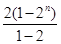 =2(2n-1), …6分
=2(2n-1), …6分
所以
S1+2S2+…+nSn=2[(2+2·22+…+n·2n)-(1+2+…+n)],
设Tn=2+2·22+…+n·2n, ①
则2Tn=22+2·23+…+n·2n+1, ②
①-②,得
-Tn=2+22+…+2n-n·2n+1=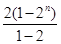 -n·2n+1=(1-n)2n+1-2,
-n·2n+1=(1-n)2n+1-2,
∴Tn=(n-1)2n+1+2, …9分
∴S1+2S2+…+nSn=2[(n-1)2n+1+2]-n(n+1)
=(n-1)2n+2+4-n(n+1). …12分
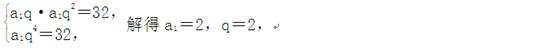 ∴an=2·2n-1=2n. …4分
∴an=2·2n-1=2n. …4分(Ⅱ)Sn=
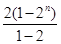 =2(2n-1), …6分
=2(2n-1), …6分所以
S1+2S2+…+nSn=2[(2+2·22+…+n·2n)-(1+2+…+n)],
设Tn=2+2·22+…+n·2n, ①
则2Tn=22+2·23+…+n·2n+1, ②
①-②,得
-Tn=2+22+…+2n-n·2n+1=
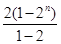 -n·2n+1=(1-n)2n+1-2,
-n·2n+1=(1-n)2n+1-2,∴Tn=(n-1)2n+1+2, …9分
∴S1+2S2+…+nSn=2[(n-1)2n+1+2]-n(n+1)
=(n-1)2n+2+4-n(n+1). …12分
本题考查等比数列的通项公式和数列求和问题。考查学生的计算能力和分析问题的能力,第一问利用基本量思想解决,第二问主抓数列的通项公式采用分组求和的方法求解.

练习册系列答案
相关题目
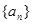 的前
的前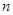 项和
项和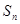 ,且
,且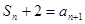
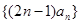 的前
的前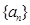 满足
满足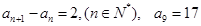 ;数列
;数列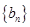 满足
满足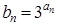
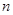 项和
项和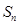 .
.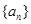 中,
中,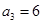 ,前三项和
,前三项和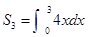 ,则公比
,则公比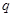 的值为( )
的值为( )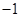 或
或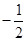
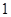 或
或 是等比数列,
是等比数列, ,则
,则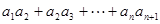 =( )
=( )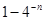 )
) (
( )
)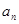 满足
满足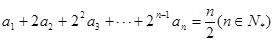
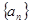 的通项;
的通项;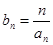 求数列
求数列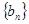 的前n项
的前n项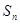 和
和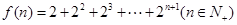 ,则
,则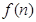 等于( )
等于( )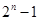
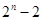
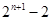
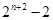
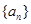 中,
中,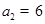 ,
,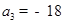 ,则
,则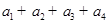 =
=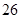

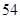

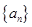 的前
的前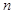 项积为
项积为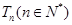 ,已知
,已知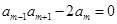 ,且
,且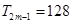 ,则
,则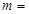 ▲ .
▲ .