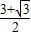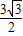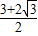题目内容
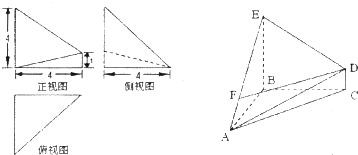
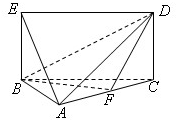 已知几何体A-BCDE如图所示,其中四边形BCDE为矩形,且BC=2,CD=
已知几何体A-BCDE如图所示,其中四边形BCDE为矩形,且BC=2,CD=| 3 |
(Ⅰ)若F为边AC上的中点,求证:AE∥平面BDF;
(Ⅱ)求此几何体A-BCDE的体积.
分析:(I)由已知中四边形BCDE为矩形,根据矩形的性质及已知中F为边AC上的中点,我们易由三角形中位线定理,得到AE∥FP,进而根据线面平行的判定定理,得到答案.
(II)取BC中点Q,连接AQ,由已知BC=2,CD=
,△ABC是边长为2的等边三角形,可得AQ⊥BC,结合平面ABC⊥平面BCDE.及面面垂直的性质定理,得到AQ⊥平面BCDE
求出棱锥的底面面积和高后,代入棱锥体积公式,即可得到答案.
(II)取BC中点Q,连接AQ,由已知BC=2,CD=
| 3 |
求出棱锥的底面面积和高后,代入棱锥体积公式,即可得到答案.
解答: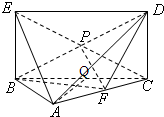 解:(Ⅰ)证明:∵四边形BCDE为矩形,∴P为EC的中点
解:(Ⅰ)证明:∵四边形BCDE为矩形,∴P为EC的中点
∵F为AC的中点,∴在△ACE中有AE∥FP
又AE?平面BDF,FP?平面BDF∴AE∥平面BDF
(Ⅱ)取BC中点Q,连接AQ
∵AQ⊥BC且AQ=
∵平面ABC⊥平面BCDE,AQ?平面BCDE,平面ABC∩平面BCDE=BC∴AQ⊥平面BCDE
∴几何体A-BCDE的体积为V=
S矩形BCDE×AQ=
×BC×CD×AQ=
×2×
×
=2
 解:(Ⅰ)证明:∵四边形BCDE为矩形,∴P为EC的中点
解:(Ⅰ)证明:∵四边形BCDE为矩形,∴P为EC的中点∵F为AC的中点,∴在△ACE中有AE∥FP
又AE?平面BDF,FP?平面BDF∴AE∥平面BDF
(Ⅱ)取BC中点Q,连接AQ
∵AQ⊥BC且AQ=
| 3 |
∵平面ABC⊥平面BCDE,AQ?平面BCDE,平面ABC∩平面BCDE=BC∴AQ⊥平面BCDE
∴几何体A-BCDE的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,其中(1)的关键,是熟练掌握线面平行的判定定理,(2)的关键是求出几何体(棱锥)的高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
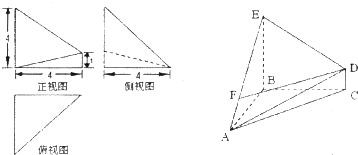
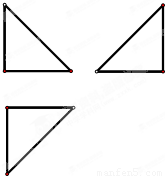
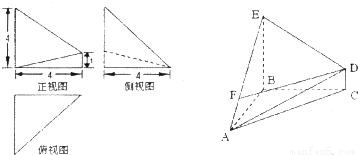
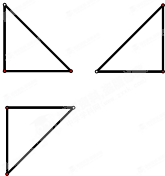 已知几何体A-BCD的三视图如图所示,其中每个图形都是腰长为1的等腰直角三角形,则该几何体的表面积为( )
已知几何体A-BCD的三视图如图所示,其中每个图形都是腰长为1的等腰直角三角形,则该几何体的表面积为( )