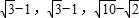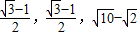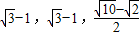题目内容
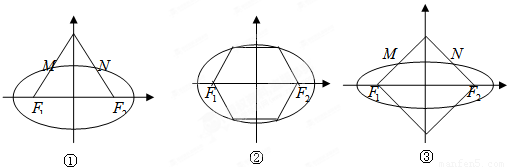
如图,三个图中的多边形都是正多边形,M,N是所在边的中点,椭圆以图中的F1、F2为焦点,设图①、图②、图③中椭圆的离心率分别是e1、e2、e3,则e1、e2、e3的值分别是( )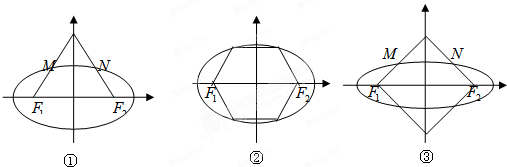

分析:根据条件,设出正多边形的边长,求出几何量a,c,即可得到离心率.
解答:解:①设等边三角形的边长为2,则椭圆的焦点为(±1,0),且过点(
,
),
∵(
,
)到两个焦点(-1,0),(1,0)的距离分别是
=
和
=1,
∴a=
,c=1,∴e1=
=
;
②设正六边形的边长为2,则椭圆的焦点为(-2,0)和(2,0),且过点(1,
),
∵点(1,
)到两个焦点(-2,0)和(2,0)的距离分别为2
和2,
∴a=
+1,c=2,∴e2=
=
;
③正方形的边长为
,则双曲线的焦点坐标为(-1,0)和(1,0),且过点(
,
).
∵点(
,
)到两个焦点(-1,0),(1,0)的距离分别是
=
和
=
,
∴a=
,c=1,∴e3=
=
.
故选B.
| 1 |
| 2 |
| ||
| 2 |
∵(
| 1 |
| 2 |
| ||
| 2 |
|
| 3 |
|
∴a=
| ||
| 2 |
| 1 | ||||
|
| ||
| 2 |
②设正六边形的边长为2,则椭圆的焦点为(-2,0)和(2,0),且过点(1,
| 3 |
∵点(1,
| 3 |
| 3 |
∴a=
| 3 |
| 2 | ||
|
| ||
| 2 |
③正方形的边长为
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵点(
| 1 |
| 2 |
| 1 |
| 2 |
|
| ||
| 2 |
|
| ||
| 2 |
∴a=
| ||||
| 4 |
| 1 | ||||||
|
| ||||
| 2 |
故选B.
点评:本题考查椭圆的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 14、有这样一种数学游戏:在3×3的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,并且每一行和每一列都不能出现重复的数字.若游戏开始时表格的第一行第一列已经填上了数字1(如图1),则此游戏有
14、有这样一种数学游戏:在3×3的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,并且每一行和每一列都不能出现重复的数字.若游戏开始时表格的第一行第一列已经填上了数字1(如图1),则此游戏有
 实数系的结构图如图所示,其中1、2、3三个方格中的内容分别为( )
实数系的结构图如图所示,其中1、2、3三个方格中的内容分别为( )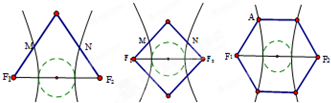 如图,三个图中的多边形都是正多边形,M,N是所在边的中点,双曲线以图中的F1,F2为焦点,则离心率分别是( )
如图,三个图中的多边形都是正多边形,M,N是所在边的中点,双曲线以图中的F1,F2为焦点,则离心率分别是( )