题目内容
(2012•杭州二模)已知动点P在直线 x+2y-1=0上,动点Q在直线 x+2y+3=0上,线段PQ中点 M(x0,y0)满足不等式
,则
的取值范围是
|
|
[
,
]
| ||
| 5 |
| 34 |
[
,
]
.
| ||
| 5 |
| 34 |
分析:首先由直线x+2y-1=0与直线x+2y+3=0是平行线,得出PQ的中点M(x0,y0)满足的直线方程;再根据
对应的平面区域进一步限定M的范围;最后结合
的几何意义求出其范围.
|
|
解答: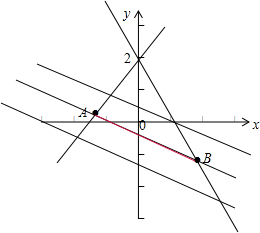 解:根据题意作图如下:
解:根据题意作图如下:
因为PQ中点为M,则点M的坐标满足方程x+2y+1=0,
又
,则点M在线段AB上,
且由方程组
和
可得 A(-3,1),B(5,-3)
而
可视为点M与原点O的距离,
其距离最小为原点到直线x+2y+1=0的距离,最大为OB.
由点到直线的距离公式可得d=
=
,
由两点间的距离公式可得d′=
=
故
的取值范围是[
,
]
故答案为:[
,
]
 解:根据题意作图如下:
解:根据题意作图如下:因为PQ中点为M,则点M的坐标满足方程x+2y+1=0,
又
|
且由方程组
|
|
而
|
其距离最小为原点到直线x+2y+1=0的距离,最大为OB.
由点到直线的距离公式可得d=
| 1 | ||
|
| ||
| 5 |
由两点间的距离公式可得d′=
| 52+(-3)2 |
| 34 |
故
|
| ||
| 5 |
| 34 |
故答案为:[
| ||
| 5 |
| 34 |
点评:本题考查两点间的距离公式,涉及距离公式几何意义的应用,属中档题.

练习册系列答案
相关题目
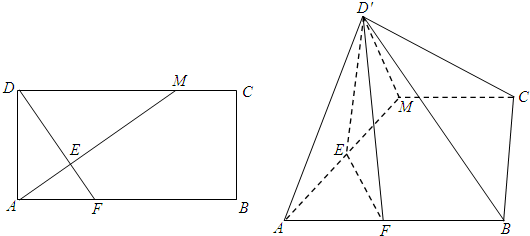
 (2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为
(2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为