题目内容
(2012•杭州二模)如图,在矩形ABCD中,AB=2BC,点M在边DC上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得四棱锥D′-ABCM.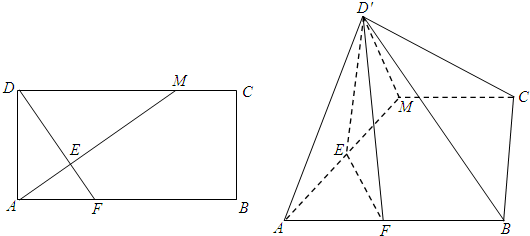
(Ⅰ)求证:AM⊥D′F;
(Ⅱ)若∠D′EF=
,直线D'F与平面ABCM所成角的大小为
,求直线AD′与平面ABCM所成角的正弦值.

(Ⅰ)求证:AM⊥D′F;
(Ⅱ)若∠D′EF=
| π |
| 3 |
| π |
| 3 |
分析:(Ⅰ)根据图形折叠前后的关系,易证AM⊥面D′EF,得出AM⊥D′F.
(Ⅱ)由(Ⅰ)知,AM⊥面D′EF,所以平面ABCM⊥面D′EF,过D′作D′H⊥EF,则D′H⊥平面ABCM,,∠D′FH是直线D'F与平面ABCM所成角,∠D′AH是直线AD′与平面ABCM所成角在直角三角形D′AH求解即可.
(Ⅱ)由(Ⅰ)知,AM⊥面D′EF,所以平面ABCM⊥面D′EF,过D′作D′H⊥EF,则D′H⊥平面ABCM,,∠D′FH是直线D'F与平面ABCM所成角,∠D′AH是直线AD′与平面ABCM所成角在直角三角形D′AH求解即可.
解答: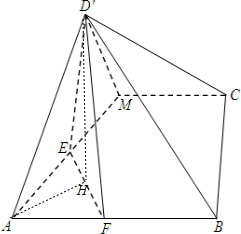 (Ⅰ)证明:∵AM⊥D′E,AM⊥EF,D′E∩⊥EF=E,
(Ⅰ)证明:∵AM⊥D′E,AM⊥EF,D′E∩⊥EF=E,
∴AM⊥面D′EF
∵D′F?面D′EF,
∴AM⊥D′F;
(Ⅱ)解:由(Ⅰ)知,AM⊥面D′EF,AM?平面ABCM,
∴平面ABCM⊥面D′EF,
∴过D′作D′H⊥EF,则D′H⊥平面ABCM,
∴∠D′FH也就是∠D′FE是直线D'F与平面ABCM所成角,由已知,∠D′FE=
,
并且∠D′AH是所求的直线AD′与平面ABCM所成角.
∵∠D′EF=
,且∠D′FE=
在三角形△D′EF中,∵∠D′EF=
,且∠D′FE=
所以是等边三角形,∴D′E=EF,即DE=EF,∴△DAF是等腰三角形.
设AD=2,∴AF=2,EF=
,四棱锥D′-ABCM的高D′H=
由于直线AD′与平面ABCM所成角为∠D′AH,∴sin∠D′AH=
=
 (Ⅰ)证明:∵AM⊥D′E,AM⊥EF,D′E∩⊥EF=E,
(Ⅰ)证明:∵AM⊥D′E,AM⊥EF,D′E∩⊥EF=E,∴AM⊥面D′EF
∵D′F?面D′EF,
∴AM⊥D′F;
(Ⅱ)解:由(Ⅰ)知,AM⊥面D′EF,AM?平面ABCM,
∴平面ABCM⊥面D′EF,
∴过D′作D′H⊥EF,则D′H⊥平面ABCM,
∴∠D′FH也就是∠D′FE是直线D'F与平面ABCM所成角,由已知,∠D′FE=
| π |
| 3 |
并且∠D′AH是所求的直线AD′与平面ABCM所成角.
∵∠D′EF=
| π |
| 3 |
| π |
| 3 |
在三角形△D′EF中,∵∠D′EF=
| π |
| 3 |
| π |
| 3 |
所以是等边三角形,∴D′E=EF,即DE=EF,∴△DAF是等腰三角形.
设AD=2,∴AF=2,EF=
| 2 |
| ||
| 2 |
由于直线AD′与平面ABCM所成角为∠D′AH,∴sin∠D′AH=
| D′H |
| D′A |
| ||
| 4 |
点评:本题考查直线与平面位置关系的判断,线面角求解,考查空间想象能力、推理论证、计算能力.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 (2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为
(2012•杭州二模)已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为