题目内容
(2013•石家庄二模)已知球0夹在一个锐二面角a-l-β之间,与两个半平面分别相切于点A、B,若AB=
,球心0到该二面角的棱l的距离为2,则球0的体积为( )
| 3 |
分析:设O、A、B三点确定的平面交棱l于点C,连接AC、CB、OC.可得∠ACB就是二面角a-l-β的平面角且OC=2,Rt△OAC中设OA=x,AC=y,利用勾股定理和等积转换,列出关于x、y的方程组.结合二面角a-l-β是锐二面角,解出半径R=OA=
,利用球的体积公式即可算出本题答案.
| 3 |
解答:解: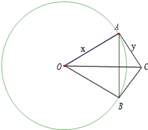 设O、A、B三点确定的平面交棱l于点C,连接AC、CB、OC
设O、A、B三点确定的平面交棱l于点C,连接AC、CB、OC
则∠ACB就是二面角a-l-β的平面角,OC长即为点O到棱l的距离,OC=2
设OA=x,AC=y,则Rt△OAC中,
解之得x=
,y=1或x=1,y=
∵二面角a-l-β是锐二面角,
∴当x=
,y=1时,∠ACB=120°不符合题意;当x=1,y=
时,∠ACB=60°符合题意
因此球0的半径R=OA=1,得球0的体积为V=
•π•13=
故选:D
 设O、A、B三点确定的平面交棱l于点C,连接AC、CB、OC
设O、A、B三点确定的平面交棱l于点C,连接AC、CB、OC则∠ACB就是二面角a-l-β的平面角,OC长即为点O到棱l的距离,OC=2
设OA=x,AC=y,则Rt△OAC中,
|
解之得x=
| 3 |
| 3 |
∵二面角a-l-β是锐二面角,
∴当x=
| 3 |
| 3 |
因此球0的半径R=OA=1,得球0的体积为V=
| 4 |
| 3 |
| 4π |
| 3 |
故选:D
点评:本题给出锐二面角的内切球,在已知切点之间的距离和球心到棱的距离情况下求球的体积.着重考查球的体积积公式和解直角三角形的知识,考查空间想象能力与计算能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目