题目内容
17.设函数f(x)=$\left\{\begin{array}{l}{{2}^{|x-1|}-1,x≥0}\\{{x}^{2}+2x+1,x<0}\end{array}\right.$,若f2(x)-(3a-1)f(x)+a2=0有5个不同的实数解,则a=2.分析 令t=f(x),方程f2(x)-(3a-1)f(x)+a2=0可化为t2-(3a-1)t+a2=0,画出函数f(x)=$\left\{\begin{array}{l}{{2}^{|x-1|}-1,x≥0}\\{{x}^{2}+2x+1,x<0}\end{array}\right.$的图象,数形结合,可得方程t2-(3a-1)t+a2=0有两个根,其中一个为1,一个为0或大于1的数,进而可得答案.
解答 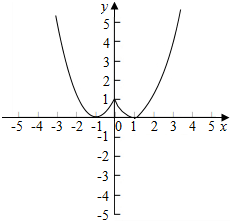 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{|x-1|}-1,x≥0}\\{{x}^{2}+2x+1,x<0}\end{array}\right.$的图象如图所示:
解:函数f(x)=$\left\{\begin{array}{l}{{2}^{|x-1|}-1,x≥0}\\{{x}^{2}+2x+1,x<0}\end{array}\right.$的图象如图所示:
令t=f(x),则方程f2(x)-(3a-1)f(x)+a2=0可化为t2-(3a-1)t+a2=0,
若方程f2(x)-(3a-1)f(x)+a2=0有5个不同的实数解,
则方程t2-(3a-1)t+a2=0有两个根,其中一个为1,一个为0或大于1的数,
将t=1代入得:1-(3a-1)+a2=0,
解得:a=1,或a=2,
当a=1时,方程t2-(3a-1)t+a2=0可化为:方程t2-2t+1=0,此时方程只有一个根1,不满足条件;
当a=2时,方程t2-(3a-1)t+a2=0可化为:方程t2-5t+4=0,此时方程一个根为1,一个根为4,满足条件;
综上所述:a=2,
故答案为:2
点评 本题考查的知识点是分段函数的应用,方程的根与函数零点的关系,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四面体ABCD中,△ABD,△ACD,△DBC和△ABC全等,且AB=AC=$\sqrt{3}$,BC=2;求证:平面BCD⊥平面ABC.
如图,在四面体ABCD中,△ABD,△ACD,△DBC和△ABC全等,且AB=AC=$\sqrt{3}$,BC=2;求证:平面BCD⊥平面ABC.