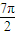题目内容
长方体的一个顶点三条棱长分别为1,2,3,该长方体的顶点都在同一个球面上,则这个球的表面积为(s=4πr2)( )
分析:由题意求出外接球的直径,求出球的半径,即可求出球的表面积.
解答:解:由题意可知长方体的外接球的直径就是长方体的体对角线的长,
由长方体的棱长可知,长方体的体对角线的长为:
=
,
所以球的直径为
,
球的半径为:
,
所以这个球的表面积为:s=4πr2=4π(
)2=14π.
故选B.
由长方体的棱长可知,长方体的体对角线的长为:
| 12+22+32 |
| 14 |
所以球的直径为
| 14 |
球的半径为:
| ||
| 2 |
所以这个球的表面积为:s=4πr2=4π(
| ||
| 2 |
故选B.
点评:本题考查几何体的外接球的表面积的求法,求出球的半径是解题的关键,考查计算能力.

练习册系列答案
相关题目