题目内容
已知
是定义在
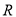上的函数，若对于任意的
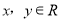，都有
，且
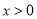，有
.
（1）求证：
；
（2）判断函数的奇偶性；
（3）判断函数
在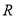
上的单调性，并证明你的结论.
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
黎明文化寒假作业系列答案寒假天地重庆出版社系列答案题目内容
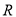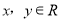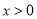已知是定义在上的函数，若对于任意的，都有，且，有.
（1）求证：；
（2）判断函数的奇偶性；
（3）判断函数在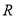上的单调性，并证明你的结论.
黎明文化寒假作业系列答案寒假天地重庆出版社系列答案
，
，则有（ ）
B.
D.
，集合
，则
与
的关系是（ ）
B.
D.
， 
满足
，实数
， 
满足
，则
的最小值为（ ）
，使
”，这个命题的否定是（ ）
，使
，使
，使
，
，
.
；
.
，且
为奇函数，若
，则
（ ）
.
的最小正周期和单调递减区间；
，求
的值.
为定义在
上的函数.
时，求
的最大值与最小值；
的最大值为
，最小值为
，设函数
，求
的解析式.