题目内容
如图,已知圆G:x2+y2-2x- y=0经过椭圆
y=0经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为 的直线l交椭圆于C,D两点,
的直线l交椭圆于C,D两点,
(Ⅰ)求椭圆的方程;
(Ⅱ)若∠CFD∈ ,求m的取值范围。
,求m的取值范围。
 y=0经过椭圆
y=0经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为 的直线l交椭圆于C,D两点,
的直线l交椭圆于C,D两点,(Ⅰ)求椭圆的方程;
(Ⅱ)若∠CFD∈
 ,求m的取值范围。
,求m的取值范围。 
解:(Ⅰ)∵圆G: 经过点F,B,
经过点F,B,
∴F(2,0),B(0, ),
),
∴c=2,b= ,
,
∴a2=6,
故椭圆的方程为 ;
;
(Ⅱ)由题意得直线l的方程为 ,
,
由 消去y得2x2-2mx+m2-6=0,
消去y得2x2-2mx+m2-6=0,
由Δ=4m2-8(m2-6)>0,解得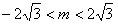 ,
,
又 ,
,
∴ ,
,
设C(x1,y1),D(x2,y2),
则x1+x2=m, ,
,
∴ ,
,
∵ (x1-2,y1),
(x1-2,y1), (x1-2,y2),
(x1-2,y2),
∴ (x1-2)(x2-2)+y1y2
(x1-2)(x2-2)+y1y2 ,
,
又椭圆方程可知 ,
,
∴
 ,
,
 ,
,
∴
 ,
,
∴
 ,
,
 ,
,
∴ ,
,
∴ ,
,
∴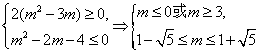
 ,
,
又 ,
,
∴ 。
。
 经过点F,B,
经过点F,B,∴F(2,0),B(0,
 ),
),∴c=2,b=
 ,
, ∴a2=6,
故椭圆的方程为
 ;
;(Ⅱ)由题意得直线l的方程为
 ,
,由
 消去y得2x2-2mx+m2-6=0,
消去y得2x2-2mx+m2-6=0,由Δ=4m2-8(m2-6)>0,解得
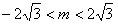 ,
,又
 ,
,∴
 ,
,设C(x1,y1),D(x2,y2),
则x1+x2=m,
 ,
, ∴
 ,
, ∵
 (x1-2,y1),
(x1-2,y1), (x1-2,y2),
(x1-2,y2),∴
 (x1-2)(x2-2)+y1y2
(x1-2)(x2-2)+y1y2 ,
,又椭圆方程可知
 ,
,∴

 ,
, ,
,∴

 ,
, ∴

 ,
, ,
,∴
 ,
, ∴
 ,
, ∴
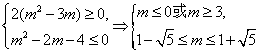
 ,
,又
 ,
,∴
 。
。
练习册系列答案
相关题目
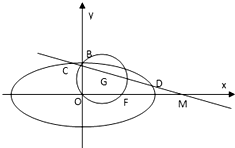 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x- 如图,已知圆G:
如图,已知圆G: