题目内容
6.已知f(x)=$\frac{2x-a}{{x}^{2}+2}$(x∈R),A=[-1,1],设关于x的方程f(x)=$\frac{1}{x}$的两根为x1,x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由.分析 由$\frac{2x-a}{{x}^{2}+2}$=$\frac{1}{x}$得x2-ax-2=0,由△=a2+8>0,知|x1-x2|=$\sqrt{{a}^{2}+8}$≤3,由此能求出实数m的取值范围.
解答 解:由$\frac{2x-a}{{x}^{2}+2}$=$\frac{1}{x}$得x2-ax-2=0.这时△=a2+8>0.
由于x1,x2是方程x2-ax-2=0的两实根,所以$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=a}\\{{x}_{1}{x}_{2}=-2}\end{array}\right.$
从而|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{a}^{2}+8}$
因为-1≤a≤1,所以|x1-x2|=$\sqrt{{a}^{2}+8}$≤3
不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立.
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立.
即m2+tm-2≥0对任意t∈[-1,1]恒成立.
设g(t)=m2+tm-2=tm+m2-2,
则g(t)≥0对任意t∈[-1,1]恒成立,故$\left\{\begin{array}{l}{g(1)≥0}\\{g(-1)≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m+{m}^{2}-2≥0}\\{-m+{m}^{2}-2≥0}\end{array}\right.$,
解得m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
点评 本小题主要考查函数的单调性,导数的应用和不等式等有关知识,考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.

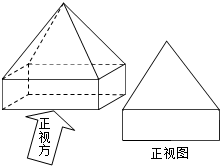
| A. |  | B. |  | C. |  | D. |  |
| A. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | B. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | ||
| C. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | D. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 |
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
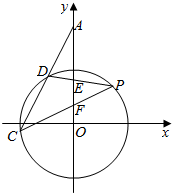 如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |
| A. | 椭圆 | B. | 圆 | C. | 线段 | D. | 射线 |