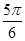题目内容
若非零向量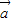 ,
,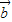 满足
满足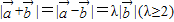 ,则
,则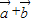 与
与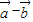 夹角的最大值为( )
夹角的最大值为( )A.
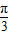
B.
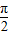
C.
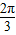
D.
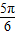
【答案】分析:由题意可得,以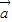 、
、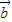 为邻边的平行四边形的两条对角线相等,都等于|
为邻边的平行四边形的两条对角线相等,都等于|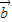 |的λ倍.设
|的λ倍.设 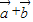 与
与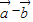 夹角为θ,由余弦定理求得 cosθ=1-
夹角为θ,由余弦定理求得 cosθ=1-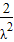 .由 λ≥2 求得 cosθ 的范围,从而求得θ的最大值.
.由 λ≥2 求得 cosθ 的范围,从而求得θ的最大值.
解答: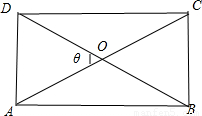 解:∵非零向量
解:∵非零向量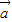 ,
,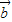 满足
满足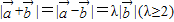 ,则以
,则以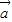 、
、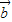 为邻边的平行四边形的两条对角线相等,都等于|
为邻边的平行四边形的两条对角线相等,都等于|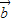 |的λ倍.
|的λ倍.
如图所示:设矩形ABCD中,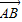 =
=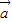 ,
,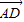 =
=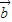 ,AC与 BD交与点O,则
,AC与 BD交与点O,则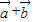 与
与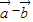 夹角等于∠AOD,
夹角等于∠AOD,
设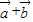 与
与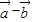 夹角为θ,|
夹角为θ,|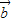 |=x,在△AOD中,由余弦定理可得 x2=
|=x,在△AOD中,由余弦定理可得 x2=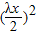 +
+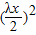 -2•
-2•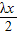 •
•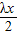 •cosθ,
•cosθ,
解得 cosθ=1-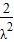 .
.
∵λ≥2,∴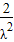 ≤
≤ ,∴cosθ≤
,∴cosθ≤ .
.
再由0≤θ≤π 可得 θ≥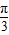 ,故θ的最大值为
,故θ的最大值为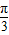 ,
,
故选A.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量夹角公式的应用,体现了数形结合的数学思想,属于中档题.
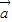 、
、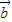 为邻边的平行四边形的两条对角线相等,都等于|
为邻边的平行四边形的两条对角线相等,都等于|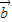 |的λ倍.设
|的λ倍.设 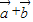 与
与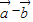 夹角为θ,由余弦定理求得 cosθ=1-
夹角为θ,由余弦定理求得 cosθ=1-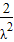 .由 λ≥2 求得 cosθ 的范围,从而求得θ的最大值.
.由 λ≥2 求得 cosθ 的范围,从而求得θ的最大值.解答:
 解:∵非零向量
解:∵非零向量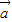 ,
,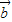 满足
满足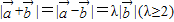 ,则以
,则以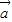 、
、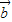 为邻边的平行四边形的两条对角线相等,都等于|
为邻边的平行四边形的两条对角线相等,都等于|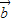 |的λ倍.
|的λ倍.如图所示:设矩形ABCD中,
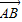 =
=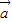 ,
,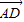 =
=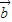 ,AC与 BD交与点O,则
,AC与 BD交与点O,则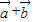 与
与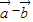 夹角等于∠AOD,
夹角等于∠AOD,设
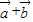 与
与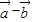 夹角为θ,|
夹角为θ,|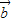 |=x,在△AOD中,由余弦定理可得 x2=
|=x,在△AOD中,由余弦定理可得 x2=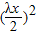 +
+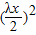 -2•
-2•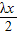 •
•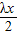 •cosθ,
•cosθ,解得 cosθ=1-
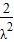 .
.∵λ≥2,∴
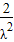 ≤
≤ ,∴cosθ≤
,∴cosθ≤ .
.再由0≤θ≤π 可得 θ≥
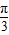 ,故θ的最大值为
,故θ的最大值为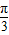 ,
,故选A.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量夹角公式的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
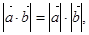 则
则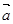 ∥
∥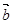 ;②
;② 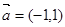 在
在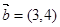 方向上的投影为
方向上的投影为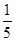 ;③若△
;③若△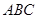 中,
中,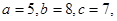 则
则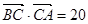 ;④若非零向量
;④若非零向量 ,则
,则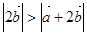 .其中所有真命题的标号是 .
.其中所有真命题的标号是 . ,则
,则 ∥
∥ ;②
;② ;③若△ABC中,a="5,b"
="8,c" =7,则
;③若△ABC中,a="5,b"
="8,c" =7,则 ·
· =20;④若非零向量
=20;④若非零向量 ,则
,则 .其中所有真命题的标号是
.其中所有真命题的标号是 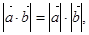 则
则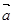 ∥
∥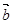 ;②
;②
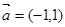 在
在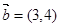 方向上的投影为
方向上的投影为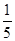 ;③若△
;③若△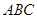 中,
中,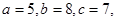 则
则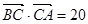 ;④若非零向量
;④若非零向量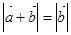 ,则
,则 .其中所有真命题的标号是 .
.其中所有真命题的标号是 . 、
、 满足
满足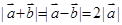 ,则
,则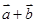 与
与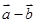 的夹角是
的夹角是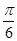 B.
B.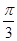 C.
C.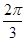 D.
D.