题目内容
有下列命题:①如果幂函数f (x)=(m2-3m+3)
 的图象不过原点,则m=l或2;
的图象不过原点,则m=l或2;②数列{an}为等比数列的充要条件为an=a1qn-1(q为常数):
③已知向量
 =(t,2),
=(t,2), =(-3,6),若向量
=(-3,6),若向量 与
与 的夹角为锐角,则实数t的取值范围是t<4;
的夹角为锐角,则实数t的取值范围是t<4; ④函数f (x)=xsinx在(0,π)上有最大值,没有最小值.
其中正确命题的个数为( )
A.0
B.1
C.2
D.3
【答案】分析:①幂函数的图象不过原点,所以幂指数小于0,系数为1,求解即可.
②根据等比数列的性质可知若数列{an}为等比数列,可以推出an=a1qn-1,反之可以利用特殊值法进行判断;
③已知向量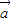 =(t,2),
=(t,2),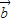 =(-3,6),根据公式cosθ=
=(-3,6),根据公式cosθ=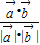 利用此信息进行求解;
利用此信息进行求解;
④求出其导数,在(0,π)上通过研究单调性的变化即可获得问题的解答;
解答:解:①幂函数y=(m2-3m+3)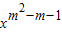 的图象不过原点,所以
的图象不过原点,所以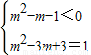 解得m=1,符合题意.故①错误;
解得m=1,符合题意.故①错误;
②若数列{an}为等比数列可以推出an=a1qn-1;若an=a1qn-1,取q=0,可得an=0,故②错误;
③向量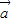 =(t,2),
=(t,2),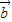 =(-3,6),若向量
=(-3,6),若向量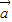 与
与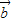 的夹角为锐角,设为θ,cosθ=
的夹角为锐角,设为θ,cosθ=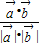 >0,即-3t+12>0解得t<4,
>0,即-3t+12>0解得t<4,
首先若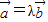 可以推出两个向量共线,此时(t,2)=λ(-3,6),可得t=-1,
可以推出两个向量共线,此时(t,2)=λ(-3,6),可得t=-1,
∴t≠-1,故t<4且t≠-1;
故③错误;
④由题意可知:f′(x)=sinx+xcosx.
当x∈(0, ),可得f′(x)>0,x∈(
),可得f′(x)>0,x∈(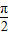 ,π),可得f′(x)<0,
,π),可得f′(x)<0,
函数在[0,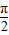 ]上单调递增,同上可知函数在(0,π)上为先增后减的函数,又所给区间为开区间,
]上单调递增,同上可知函数在(0,π)上为先增后减的函数,又所给区间为开区间,
∴函数f (x)=xsinx在(0,π)上有最大值,没有最小值.
故④正确;
故选B;
点评:本题考查的是函数的性质分析问题.在解答的过程当中成分体现了导数的知识、函数最值的知识、向量的内积.值得同学们体会和反思.
②根据等比数列的性质可知若数列{an}为等比数列,可以推出an=a1qn-1,反之可以利用特殊值法进行判断;
③已知向量
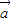 =(t,2),
=(t,2),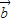 =(-3,6),根据公式cosθ=
=(-3,6),根据公式cosθ=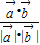 利用此信息进行求解;
利用此信息进行求解;④求出其导数,在(0,π)上通过研究单调性的变化即可获得问题的解答;
解答:解:①幂函数y=(m2-3m+3)
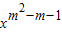 的图象不过原点,所以
的图象不过原点,所以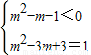 解得m=1,符合题意.故①错误;
解得m=1,符合题意.故①错误;②若数列{an}为等比数列可以推出an=a1qn-1;若an=a1qn-1,取q=0,可得an=0,故②错误;
③向量
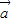 =(t,2),
=(t,2),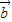 =(-3,6),若向量
=(-3,6),若向量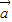 与
与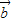 的夹角为锐角,设为θ,cosθ=
的夹角为锐角,设为θ,cosθ=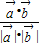 >0,即-3t+12>0解得t<4,
>0,即-3t+12>0解得t<4,首先若
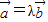 可以推出两个向量共线,此时(t,2)=λ(-3,6),可得t=-1,
可以推出两个向量共线,此时(t,2)=λ(-3,6),可得t=-1,∴t≠-1,故t<4且t≠-1;
故③错误;
④由题意可知:f′(x)=sinx+xcosx.
当x∈(0,
 ),可得f′(x)>0,x∈(
),可得f′(x)>0,x∈(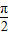 ,π),可得f′(x)<0,
,π),可得f′(x)<0,函数在[0,
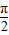 ]上单调递增,同上可知函数在(0,π)上为先增后减的函数,又所给区间为开区间,
]上单调递增,同上可知函数在(0,π)上为先增后减的函数,又所给区间为开区间,∴函数f (x)=xsinx在(0,π)上有最大值,没有最小值.
故④正确;
故选B;
点评:本题考查的是函数的性质分析问题.在解答的过程当中成分体现了导数的知识、函数最值的知识、向量的内积.值得同学们体会和反思.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 的图象不过原点,则m=l或2;
的图象不过原点,则m=l或2; =(t,2),
=(t,2), =(-3,6),若向量
=(-3,6),若向量 与
与 的夹角为锐角,则实数t的取值范围是t<4;
的夹角为锐角,则实数t的取值范围是t<4;