题目内容
（本小题满分12分）
（文科）已知二次函数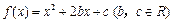
，且
．
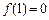（1）若函数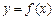
与x轴的两个交点
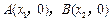之间的距离为2，求b的值；
（2）若关于x的方程
的两个实数根分别在区间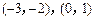
内，求b的取值范围．
解：(1) 由题可知，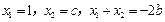
又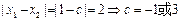
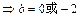
(2) 令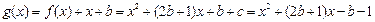
由题，
解析
练习册系列答案
相关题目
的定义域为
，且满足条件：①
，②
③当
.
的解集
＝x2＋2x－5，x∈[t，t＋1]，若f(x)的最小值为h(t)，写出h(t)的表达式．
lg2+
-
÷
；
的值.
＝
＋
有如下性质：如果常数
＞0，那么该
0，
上是减函数，在
上是增函数．
（
的值；
＋
（常数
＞0）在定义域内的单调性，并说明理由；
（常数
＝
＋
（
是正整数）在区间[
，2]上的最大值和最小值（可利用你
为偶函数，曲线
过点
，
．
存在斜率为0的切线，求实数
的取值范围；
时函数
(x≠0，常数a∈R).
，其中m为R上的常数，若函数
在x=1处取得极大值0，
，若对
恒成立，．函数
是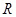
上的可导函数,
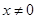时，
，则函数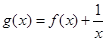
的零点个数为（ ）
A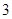． | B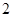． | C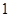． | D． |
题目内容
（本小题满分12分）
（文科）已知二次函数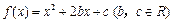，且．
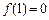（1）若函数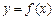与x轴的两个交点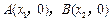之间的距离为2，求b的值；
（2）若关于x的方程的两个实数根分别在区间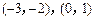内，求b的取值范围．
解：(1) 由题可知，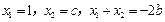
又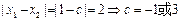
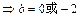
(2) 令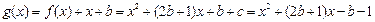
由题，
解析
．函数是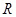上的可导函数,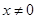时，，则函数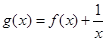的零点个数为（ ）
| A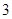． | B． | C． | D． |