题目内容
已知双曲线E的中心在原点,焦点在坐标轴上,离心率e=
,且双曲线过点P(2,3
),求双曲线E的方程.
| ||
| 2 |
| 2 |
分析:根据双曲线的离心率设出双曲线的方程,考虑到焦点在x轴和在y轴两种情况,再代入点P(2,3
),求出双曲线方程即可.
| 2 |
解答:解:由双曲线离心率e=
,当焦点在y轴时,设双曲线的方程为
-
=λ
代入点P(2,3
),解得,λ=
,
故双曲线的方程为
-
=1
当焦点在x轴时,设双曲线的方程为
-
=λ,
代入点P(2,3
),解得,λ=-7,舍
故双曲线的方程为
-
=1.
| ||
| 2 |
| y2 |
| 4 |
| x2 |
| 2 |
代入点P(2,3
| 2 |
| 5 |
| 2 |
故双曲线的方程为
| y2 |
| 10 |
| x2 |
| 5 |
当焦点在x轴时,设双曲线的方程为
| x2 |
| 4 |
| y2 |
| 2 |
代入点P(2,3
| 2 |
故双曲线的方程为
| y2 |
| 10 |
| x2 |
| 5 |
点评:本题考查了求双曲线的标准方程,设出标准形式,求出参数即可,属于基础题型.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
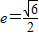 ,且双曲线过点
,且双曲线过点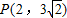 ,求双曲线E的方程.
,求双曲线E的方程.