题目内容
已知A（1，1）为椭圆
=1内一点，F1为椭圆左焦点，P为椭圆上一动点
求｜PF1｜+｜PA｜的最大值和最小值.
｜PF1｜+｜PA｜的最大值是6+
,最小值是6–
解析:
由
可知a=3,b=
,c=2，左焦点F1(–2,0),右焦点F2(2,0)
由椭圆定义，｜PF1｜=2a–｜PF2｜=6–｜PF2｜,
∴｜PF1｜+｜PA｜=6–｜PF2｜+｜PA｜=6+｜PA｜–｜PF2｜
如图:
由｜｜PA｜–｜PF2｜｜≤｜AF2｜=
知
–≤｜PA｜–｜PF2｜≤.
当P在AF2延长线上的P2处时，取右“=”号；
当P在AF2的反向延长线的P1处时，取左“=”号.
即｜PA｜–｜PF2｜的最大、最小值分别为，–.
于是｜PF1｜+｜PA｜的最大值是6+,最小值是6–.
练习册系列答案
相关题目
（其中
为一正实数)到实数集R上的映射过程：区间
对应线段
上的点
，如图1；将线段
的椭圆，使两端点
、
恰好重合于椭圆的一个短轴端点，如图2 ；再将这个椭圆放在平面直角坐标系中，使其中心在坐标原点，长轴在
轴上，已知此时点
，如图3，在图形变化过程中，图1中线段
的长度对应于图3中的椭圆弧ADM的长度.图3中直线
交于点
，则与实数
，记作
,
；
②函数
是奇函数；③函数
上单调递增； ④.函数
对称；⑤函数
时AM过椭圆的右焦点.其中所有的真命题是: （ ）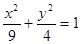
与坐标轴正半轴的两个交点.
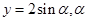为参数，求椭圆的参数方程；
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．