题目内容
如果一个钝角三角形的边长是三个连续自然数,那么最长边的长度为( )
| A．3 | B．4 | C．6 | D．7 |
B
设出三边的长度,然后由余弦定理,使其最长边所对的角的余弦值小于0即可得到边长的取值范围,再结合边长是自然数得到解.
设三角形的三边长分别为n-1,n,n+1(n>1),则n+1对的角θ为钝角,由余弦定理得cosθ=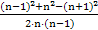
,所以(n-1)2+n2<(n+1)2,解得0<n<4,所以n=2,3.当n=2时,三边长为1,2,3,1+2=3,不符合题意.当n=3时,三边长为2,3,4,符合题意.故最长边的长度为4.
设三角形的三边长分别为n-1,n,n+1(n>1),则n+1对的角θ为钝角,由余弦定理得cosθ=
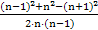,所以(n-1)2+n2<(n+1)2,解得0<n<4,所以n=2,3.当n=2时,三边长为1,2,3,1+2=3,不符合题意.当n=3时,三边长为2,3,4,符合题意.故最长边的长度为4.
练习册系列答案
相关题目
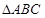中，角A、B、C的对边分别为a、b、c，S是该三角形的面积
，
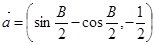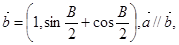求角B的度数
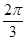，S=
，求b的值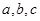
，若A,B,C成等差数列，
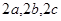成等比数列，则
（ ）
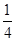
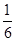
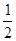
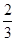
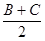,1）,n="(-2,cos" 2A+1),且m⊥n.
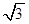,且△ABC的面积S=
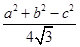时,求边c的值和△ABC的面积.
，AC＝
，点P是△ABC的外接圆上的一个动点，则
·
的最大值是________．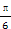
,S△ABC=
,则b= .
为双曲线
的左，右焦点，点
在该双曲线上，且
，则
="(" )
中，内角
的对边长分别是
，若
，则角
的大小为