题目内容
等轴双曲线过(4,-
)点
(1)求双曲线的标准方程;
(2)求该双曲线的离心率和焦点坐标.
| 7 |
(1)求双曲线的标准方程;
(2)求该双曲线的离心率和焦点坐标.
分析:(1)因为双曲线为等轴双曲线,所以设双曲线方程为x2-y2=λ(λ≠0),又双曲线过(4,-
)点,即可求得λ的值,得到双曲线的标准方程;
(2)由等轴双曲线,得到该双曲线的离心率,由求出的双曲线方程即可得到交点坐标.
| 7 |
(2)由等轴双曲线,得到该双曲线的离心率,由求出的双曲线方程即可得到交点坐标.
解答:解:(1)设为x2-y2=λ(λ≠0)
将(4,-
)代入双曲线方程得λ=9,
∴双曲线的标准方程为
-
=1
(2)∵该双曲线是等轴双曲线,∴离心率e=
,
∵a=3,c=
a,焦点在x轴上,
∴焦点坐标为(3
,0),(-3
,0).
将(4,-
| 7 |
∴双曲线的标准方程为
| x2 |
| 9 |
| y2 |
| 9 |
(2)∵该双曲线是等轴双曲线,∴离心率e=
| 2 |
∵a=3,c=
| 2 |
∴焦点坐标为(3
| 2 |
| 2 |
点评:本题主要考查了等轴双曲线的方程的求法,做题时应用到等轴双曲线可设为x2-y2=λ(λ≠0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
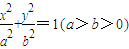 的离心率与等轴双曲线的离心率互为倒数关系,直线
的离心率与等轴双曲线的离心率互为倒数关系,直线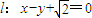 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.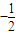 ,-1).
,-1).