题目内容
已知椭圆C: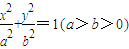 的离心率与等轴双曲线的离心率互为倒数关系,直线
的离心率与等轴双曲线的离心率互为倒数关系,直线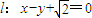 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.(I)求椭圆C的方程;
(Ⅱ)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点(
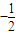 ,-1).
,-1).
【答案】分析:(I)由等轴双曲线的离心率为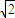 ,可得椭圆的离心率
,可得椭圆的离心率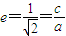 .因为直线
.因为直线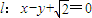 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,利用点到直线的距离公式和直线与圆相切的性质可得
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,利用点到直线的距离公式和直线与圆相切的性质可得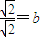 ,再利用a2=b2+c2即可得出;
,再利用a2=b2+c2即可得出;
(II)分直线AB的斜率不存在与存在两种情况讨论,①不存在时比较简单;②斜率存在时,设直线AB的方程为y=kx+m,由椭圆m≠±1.与椭圆的方程联立,利用根与系数的关系及斜率公式,再利用k1+k2=4即可证明.
解答:(I)解:∵等轴双曲线的离心率为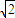 ,∴椭圆的离心率
,∴椭圆的离心率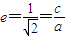 ,
,
又∵直线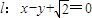 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,
∴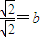 ,即b=1,
,即b=1,
联立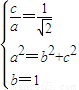 ,解得
,解得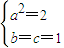 ,
,
∴椭圆C的方程为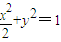 .
.
(II)证明:由(I)可知:M(0,1).
①若直线AB的斜率不存在,设方程为x=x,则A(x,y),B(x,-y).
由已知得 ,解得
,解得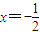 ,
,
此时直线AB的方程为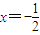 ,显然过点
,显然过点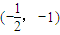 .
.
②若直线AB的斜率存在,设直线AB的方程为y=kx+m,由椭圆m≠±1.
设A(x1,y1),B(x2,y2).联立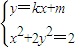 .
.
化为(1+2k2)x2+4kmx+2m2-2=0,
∴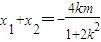 ,
, .(*)
.(*)
∵k1+k2=4,∴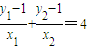 ,
,
∴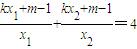 ,化为
,化为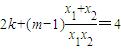 .
.
把(*)代入得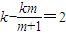 ,∴k=2(m+1),∴
,∴k=2(m+1),∴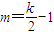 .
.
∴直线AB的方程为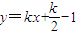 ,即
,即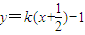 ,
,
∴直线AB过定点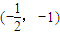 .
.
点评:熟练掌握椭圆与原点的标准方程及其性质、直线与圆性质的性质、点到直线的距离公式、直线 与椭圆相交问题转化为方程联立化为一元二次方程点到根与系数的关系、直线的斜率计算公式等是解题的关键.
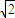 ,可得椭圆的离心率
,可得椭圆的离心率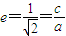 .因为直线
.因为直线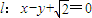 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,利用点到直线的距离公式和直线与圆相切的性质可得
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,利用点到直线的距离公式和直线与圆相切的性质可得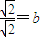 ,再利用a2=b2+c2即可得出;
,再利用a2=b2+c2即可得出;(II)分直线AB的斜率不存在与存在两种情况讨论,①不存在时比较简单;②斜率存在时,设直线AB的方程为y=kx+m,由椭圆m≠±1.与椭圆的方程联立,利用根与系数的关系及斜率公式,再利用k1+k2=4即可证明.
解答:(I)解:∵等轴双曲线的离心率为
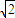 ,∴椭圆的离心率
,∴椭圆的离心率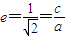 ,
,又∵直线
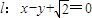 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,∴
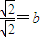 ,即b=1,
,即b=1,联立
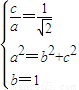 ,解得
,解得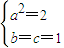 ,
,∴椭圆C的方程为
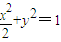 .
.(II)证明:由(I)可知:M(0,1).
①若直线AB的斜率不存在,设方程为x=x,则A(x,y),B(x,-y).
由已知得
 ,解得
,解得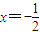 ,
,此时直线AB的方程为
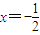 ,显然过点
,显然过点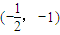 .
.②若直线AB的斜率存在,设直线AB的方程为y=kx+m,由椭圆m≠±1.
设A(x1,y1),B(x2,y2).联立
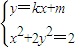 .
.化为(1+2k2)x2+4kmx+2m2-2=0,
∴
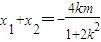 ,
, .(*)
.(*)∵k1+k2=4,∴
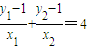 ,
,∴
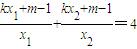 ,化为
,化为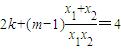 .
.把(*)代入得
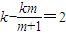 ,∴k=2(m+1),∴
,∴k=2(m+1),∴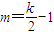 .
.∴直线AB的方程为
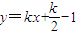 ,即
,即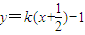 ,
,∴直线AB过定点
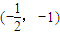 .
.点评:熟练掌握椭圆与原点的标准方程及其性质、直线与圆性质的性质、点到直线的距离公式、直线 与椭圆相交问题转化为方程联立化为一元二次方程点到根与系数的关系、直线的斜率计算公式等是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、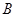 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.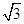
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线