题目内容
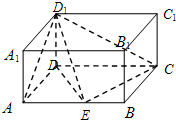 如图在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上的动点.
如图在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上的动点.(1)若异面直线AD1与EC所成角为600,试确定此时动点E的位置.
(2)求三棱锥C-DED1的体积.
分析:(1)以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系则E(1,t,0)则A(1,0,0),D(0,0,0),D1(0,0,1),C(0,2,0),由向量法能求出异面直线AD1与EC所成角的大小列出等式即可求出t.
(2)设点C到平面DED1的距离为h,能求出点C到平面D1DE的距离为1,再求得底面面积,根据锥体的体积公式求解即得.
(2)设点C到平面DED1的距离为h,能求出点C到平面D1DE的距离为1,再求得底面面积,根据锥体的体积公式求解即得.
解答:解:(1)以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系
设:E(1,t,0)则A(1,0,0),D(0,0,0),D1(0,0,1),C(0,2,0),
=(1,0,-1)
=(1,t-2,0),4分
根据数量积的定义及已知得:
∴1+0•(t-2)+0=
•
•cos60°.
t=1,∴E的位置是AB中点.7分
(2)VC-DED1=VD1-DEC=
•
•2•1•1=
,14分.
设:E(1,t,0)则A(1,0,0),D(0,0,0),D1(0,0,1),C(0,2,0),
| D1A |
| CE |
根据数量积的定义及已知得:
∴1+0•(t-2)+0=
| 2 |
| 1+(t-2)2 |
t=1,∴E的位置是AB中点.7分
(2)VC-DED1=VD1-DEC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查空间直角坐标系、异面直线所成角、棱柱、棱锥、棱台的体积的计算,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
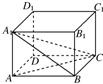 6、如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为( )
6、如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为( ) 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: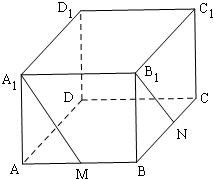 如图在长方体ABCD-A1B1C1D1中,AB=a,AD=b,AC1=c,点M为AB的中点,点N为BC的中点.
如图在长方体ABCD-A1B1C1D1中,AB=a,AD=b,AC1=c,点M为AB的中点,点N为BC的中点.