题目内容
17.下列四个命题:①“ax<ay(0<a<1)”成立的充要条件是“ln(x2+1)>ln(y2+1)”;
②命题“若x>y,则-x<-y”的逆否命题是“若-x>-y,则x<y”;
③设$\overrightarrow a,\overrightarrow b$是任意两个向量,则“$\overrightarrow a•\overrightarrow b=|\overrightarrow a||\overrightarrow b|$”是“$\overrightarrow a∥\overrightarrow b$”的充分不必要条件;
④把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移$\frac{π}{8}$个单位即可得到函数$y=sin({-2x+\frac{π}{4}})$(x∈R)的图象.
其中正确命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 ①“ax<ay(0<a<1)”成立的充要条件是x>y,而“ln(x2+1)>ln(y2+1)”?|x|>|y|,即可判断出正误;
②利用逆否命题的定义即可判断出正误;
③设$\overrightarrow a,\overrightarrow b$是任意两个向量,则“$\overrightarrow a•\overrightarrow b=|\overrightarrow a||\overrightarrow b|$”?“$\overrightarrow a∥\overrightarrow b$”且方向相同,即可判断出正误;
④把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移$\frac{π}{8}$个单位即可得到函数y=$sin[-2(x-\frac{π}{8})]$=$sin(-2x+\frac{π}{4})$(x∈R)的图象,即可判断出正误.
解答 解:①“ax<ay(0<a<1)”成立的充要条件是x>y,而“ln(x2+1)>ln(y2+1)”?|x|>|y|,因此不正确;
②命题“若x>y,则-x<-y”的逆否命题是“若-x≥-y,则x≤y”,因此不正确;
③设$\overrightarrow a,\overrightarrow b$是任意两个向量,则“$\overrightarrow a•\overrightarrow b=|\overrightarrow a||\overrightarrow b|$”?“$\overrightarrow a∥\overrightarrow b$”且方向相同,因此“$\overrightarrow a•\overrightarrow b=|\overrightarrow a||\overrightarrow b|$”是“$\overrightarrow a∥\overrightarrow b$”的充分不必要条件,正确;
④把函数y=sin(-2x)(x∈R)的图象上所有的点向右平移$\frac{π}{8}$个单位即可得到函数y=$sin[-2(x-\frac{π}{8})]$=$sin(-2x+\frac{π}{4})$(x∈R)的图象,正确.
其中正确命题的个数是2.
故选:C.
点评 本题考查了函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
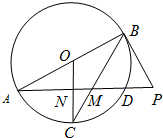 如图AB是圆O的直径,过B作圆O的切线交弦AD的延长线于点P,M为AD上一点,且PB=PM=6,PD=4,连接BM并延长交圆O于点C,连接OC交AD于点N,则CN=$\frac{{\sqrt{5}}}{2}$.
如图AB是圆O的直径,过B作圆O的切线交弦AD的延长线于点P,M为AD上一点,且PB=PM=6,PD=4,连接BM并延长交圆O于点C,连接OC交AD于点N,则CN=$\frac{{\sqrt{5}}}{2}$. 在平面直角坐标系xoy中,已知椭圆C的方程为$\frac{{x}^{2}}{8}$+y2=1,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不 重合的点.
在平面直角坐标系xoy中,已知椭圆C的方程为$\frac{{x}^{2}}{8}$+y2=1,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不 重合的点.