题目内容
某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算该射手在一次射击中:
(1)射中10环或9环的概率;
(2)少于7环的概率。
(1)射中10环或9环的概率;
(2)少于7环的概率。
(1)0.44;(2)0.03.
本试题主要考查了互斥事件的概率的加法公式的运用。第一问射中10环或9环的概即为0.21+0.23=0.44
第二问中,少于7环的概率等于1减去大于等于7环的概率值,即为
1-(0.21+0.23+0.25+0.28)=0.03
解:(1)因为在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28所以说设射中10环或9环的为事件A,则P(A)=0.21+0.23=0.44
(2)设大于等于7环为事件B,则少于7环的概率1-P(B)=1-(0.21+0.23+0.25+0.28)=0.03
第二问中,少于7环的概率等于1减去大于等于7环的概率值,即为
1-(0.21+0.23+0.25+0.28)=0.03
解:(1)因为在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28所以说设射中10环或9环的为事件A,则P(A)=0.21+0.23=0.44
(2)设大于等于7环为事件B,则少于7环的概率1-P(B)=1-(0.21+0.23+0.25+0.28)=0.03

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
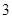 名男生
名男生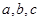 和
和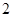 名女生
名女生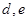 中任选
中任选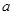 被选中的概率
被选中的概率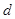 至少一人被选中的概率。
至少一人被选中的概率。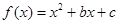 ,其中
,其中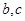 是某范围内的随机数,分别在下列条件下,求事件A “
是某范围内的随机数,分别在下列条件下,求事件A “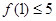 且
且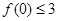 ”发生的概率.
”发生的概率.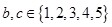 ;
;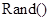 产生的随机数的范围为
产生的随机数的范围为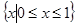 ,
,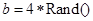 和
和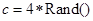 的执行结果.(注: 符号“
的执行结果.(注: 符号“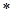 ”表示“乘号”)
”表示“乘号”)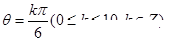 ,则
,则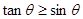 的概率为( )
的概率为( )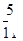
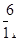
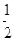




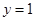 和
和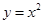 所围成的部分)的面积S时,若向矩形ABCD内随机撒1000粒豆子,落在阴影区域内的有698粒,由此可得S的近似值
所围成的部分)的面积S时,若向矩形ABCD内随机撒1000粒豆子,落在阴影区域内的有698粒,由此可得S的近似值 上随机取一个数
上随机取一个数 ,
, 的值介于0到
的值介于0到 之间的概率为
之间的概率为


 ,任取一点
,任取一点 ,使
,使 的概率( )
的概率( )


