题目内容
已知双曲线C与曲线
-
=1有公共的渐近线,且经过点A(-3,4
),则C的方程为
-
=1
-
=1.
| x2 |
| 9 |
| y2 |
| 16 |
| 2 |
| y2 |
| 16 |
| x2 |
| 9 |
| y2 |
| 16 |
| x2 |
| 9 |
分析:与双曲线
-
=1共渐近线的双曲线方程可设为
-
=λ(其中λ≠0),因此设本题中的双曲线C的方程为
-
=λ,再代入点A的坐标即可得到双曲线C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 9 |
| y2 |
| 16 |
解答:解:设双曲线C的方程为
-
=λ,其中λ≠0
∵点A(-3,4
)在双曲线C上,
∴
-
=λ,解之得λ=-1
因此双曲线方程为
-
=-1,即
-
=1
故答案为:
-
=1
| x2 |
| 9 |
| y2 |
| 16 |
∵点A(-3,4
| 2 |
∴
| (-3)2 |
| 9 |
(4
| ||
| 16 |
因此双曲线方程为
| x2 |
| 9 |
| y2 |
| 16 |
| y2 |
| 16 |
| x2 |
| 9 |
故答案为:
| y2 |
| 16 |
| x2 |
| 9 |
点评:本题给出与已知双曲线共渐近线的双曲线经过某个已知点,求该双曲线的方程,着重考查了双曲线的标准方程与简单几何性质,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
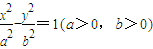 ,它的左、右焦点分别F1,F2,左右顶点为A1,A2,过焦点F2先做其渐近线的垂线,垂足为p,再作与x轴垂直的直线与曲线C交于点Q,R,若PF2,A1A2,QF1依次成等差数列,则离心率e=( )
,它的左、右焦点分别F1,F2,左右顶点为A1,A2,过焦点F2先做其渐近线的垂线,垂足为p,再作与x轴垂直的直线与曲线C交于点Q,R,若PF2,A1A2,QF1依次成等差数列,则离心率e=( )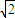
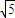
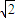 或
或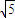
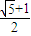
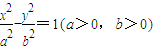 的一个焦点是F2(2,0),且
的一个焦点是F2(2,0),且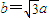 .
.