题目内容
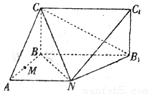
 如图已知:BA,BC,BB1两两垂直,BCC1B1为矩形,ABB1N为直角梯形,BC=BA=AN=4,BB1=8.
如图已知:BA,BC,BB1两两垂直,BCC1B1为矩形,ABB1N为直角梯形,BC=BA=AN=4,BB1=8.(I)证明:BN⊥平面C1B1N;
(ll)求二面角C-NB1-C1的余弦值,
(III )M为AB的中点,在线段CB上是否存在一点P,使得MP∥平面CNB1,若存在,求出BP的长;若不存在,请说明理由.
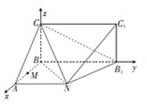
分析:(I)以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系,则
=(4,4,0),
=(-4,4,0),
=(0,0,4),所以
•
=0,
•
=0,由此能够证明BN⊥平面C1B1N.
(II)由BN⊥平面C1B1N,知
=(4,4,0)是平面C1B1N的一个法向量,再求出平面CB1N的一个法向量
=(1,1,2),利用向量法能够求出二面角C-NB1-C1的余弦值.
(III)由M(2,0,0),设P(0,0,a)(0≤a≤4)为BC上一点,则
=(-2,0,a),由MP∥平面CNB1,
⊥
,能求出占点P坐标和BP的长.
| BN |
| NB1 |
| B1C1 |
| BN |
| NB1 |
| BN |
| B1C1 |
(II)由BN⊥平面C1B1N,知
| BN |
| n |
(III)由M(2,0,0),设P(0,0,a)(0≤a≤4)为BC上一点,则
| MP |
| MP |
| n |
解答:解:(I)以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系,
则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4),
∴
=(4,4,0),
=(-4,4,0),
=(0,0,4),
∴
•
=0,
•
=0,
∴BN⊥NB1,BN⊥B1C1,
∵NB1∩B1C1=B1,
∴BN⊥平面C1B1N.
(II)∵BN⊥平面C1B1N,
∴
=(4,4,0)是平面C1B1N的一个法向量,
设平面CB1N的一个法向量为
=(x,y,z),则
•
=0,
•
=0,
∴
,解得
=(1,1,2),
设二面角C-NB1-C1的平面角为θ,
则cosθ=|cos<
,
>|=|
|=
,
∴二面角C-NB1-C1的余弦值为
.
(III)∵M(2,0,0),设P(0,0,a)(0≤a≤4)为BC上一点,
则
=(-2,0,a),
∵MP∥平面CNB1,
⊥
,
∴
•
=-2+2a=0,解得a=1,
∴在BC上存在一点P(0,0,1),MP∥平面CNB1,且BP=1.
则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4),
∴
| BN |
| NB1 |
| B1C1 |
∴
| BN |
| NB1 |
| BN |
| B1C1 |
∴BN⊥NB1,BN⊥B1C1,
∵NB1∩B1C1=B1,
∴BN⊥平面C1B1N.

(II)∵BN⊥平面C1B1N,
∴
| BN |
设平面CB1N的一个法向量为
| n |
| n |
| CN |
| n |
| B1N |
∴
|
| n |
设二面角C-NB1-C1的平面角为θ,
则cosθ=|cos<
| BN |
| n |
| 4+4 | ||||
|
| ||
| 3 |
∴二面角C-NB1-C1的余弦值为
| ||
| 3 |
(III)∵M(2,0,0),设P(0,0,a)(0≤a≤4)为BC上一点,
则
| MP |
∵MP∥平面CNB1,
| MP |
| n |
∴
| MP |
| n |
∴在BC上存在一点P(0,0,1),MP∥平面CNB1,且BP=1.
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,探索满足条件的点是否存在.解题时要认真审题,仔细解答,注意等价转化思想和向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
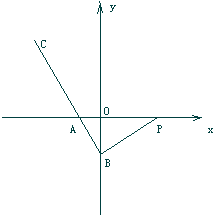 如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使
如图,已知直角三角形PAB的直角顶点为B,点P的坐标为(3,0),点B在y轴上,点A在x轴的负半轴上,在BA的延长线上取一点C,使