题目内容
（不等式选讲选做题）已知2x2+3y2=6，则|x|+
y的最大值M=
| 3 |
3
3
．分析：由已知方程2x2+3y2=6是椭圆的标准方程，故考虑使用三角换元法求函数的最值，或者说使用椭圆的参数方程将所求二元函数转化为一元函数求最值即可
解答：解：∵2x2+3y2=6，∴设x=
cosθ，y=
sinθ
则f（θ）=|x|+
y=
|cosθ|+
sinθ
cosθ＞0时，f（θ）=
cosθ+
sinθ=3sin（θ+φ）≤3 （其中sinφ=
，cosφ=
，cosθ=sinφ=
时取等号）
cosθ≤0时，f（θ）=-
cosθ+
sinθ=3sin（θ+η）≤3 （其中sinη=-
，cosη=
，cosθ=sinη=-
时取等号）
∴|x|+
y的最大值M=3
故答案为3
| 3 |
| 2 |
则f（θ）=|x|+
| 3 |
| 3 |
| 6 |
cosθ＞0时，f（θ）=
| 3 |
| 6 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
cosθ≤0时，f（θ）=-
| 3 |
| 6 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴|x|+
| 3 |
故答案为3
点评：本题考察了椭圆的标准方程和参数方程及其应用，转化化归的思想方法，三角函数求最值的方法
练习册系列答案
阅读快车系列答案
相关题目
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
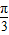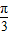）的直角坐标是 ．