题目内容
已知钝角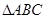 的三边的长是3个连续的自然数,其中最大角为
的三边的长是3个连续的自然数,其中最大角为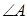 ,则
,则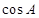 =_____
=_____
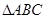 的三边的长是3个连续的自然数,其中最大角为
的三边的长是3个连续的自然数,其中最大角为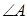 ,则
,则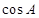 =_____
=_____ 
试题分析:不妨设三边满足a<b<c,满足a=n-1,b=n,c=n+1(n≥2,n∈N).根据余弦定理以及角C为钝角,建立关于n的不等式并解之可得0<n<4,再根据n为整数和构成三角形的条件,可得出本题答案。解:不妨设三边满足a<b<c,满足a=n-1,b=n,c=n+1(n≥2,n∈N).∵△ABC是钝角三角形,∴可得∠C为钝角,即cosC<0,由余弦定理得:(n+1)2=(n-1)2+n2-2n(n-1)•cosC>(n-1)2+n2,即(n-1)2+n2<(n+1)2,化简整理得n2-4n<0,解之得0<n<4,∵n≥2,n∈N,∴n=2,n=3,当n=2时,不能构成三角形,舍去,当n=3时,△ABC三边长分别为2,3,4,
 故答案为
故答案为
点评:本题属于解三角形的题型,涉及的知识有三角形的边角关系,余弦函数的图象与性质以及余弦定理,属于基础题.灵活运用余弦定理解关于n的不等式,并且寻找整数解,是解本题的关键.

练习册系列答案
相关题目
 , B=
, B= ,
, =1,求
=1,求 和A、C.
和A、C. 的内角
的内角 所对的边分别为
所对的边分别为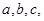 且
且 。
。 ,求
,求 的值;
的值; ,求
,求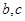 的值。
的值。 .
.  的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则 )
)



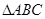 中,a,b,c分别是角A,B,C的对边,已知
中,a,b,c分别是角A,B,C的对边,已知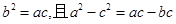
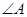 的大小;
的大小;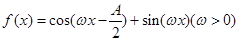 且
且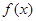 的最小正周期为
的最小正周期为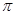 ,求
,求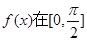 的最大值。
的最大值。 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
, .
.  ,求
,求 的值.
的值.