题目内容
【题目】已知函数f(x)=a(x﹣1)﹣lnx(a∈R),g(x)=(1﹣x)ex.
(1)讨论函数f(x)的单调性;
(2)若对任意给定的x0∈[﹣1,1],在区间(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
【答案】(1)答案见解析;(2)[![]() ,+∞)
,+∞)
【解析】
(1)首先求出函数的导数,分a≤0和a>0两种情况讨论,然后根据导数与单调区间的关系确定函数的单调区间;
(2)首先利用导数求出g(x)的值域为[0,1],根据(1)可排除a≤0和0<a![]() 的情况,由函数f(x)的单调性和图象分析可知,a满足以下条件
的情况,由函数f(x)的单调性和图象分析可知,a满足以下条件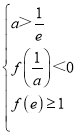 时符合题意,结合构造函数求解不等式即可得到结果.
时符合题意,结合构造函数求解不等式即可得到结果.
(1)f(x)=a(x﹣1)﹣lnx,x>0,则f′(x)=a![]() ,
,
①当a≤0时,f′(x)<0,函数f(x)在(0,+∞)上为减函数,
②当a>0时,令f′(x)>0得x![]() ,令f′(x)<0得0<x
,令f′(x)<0得0<x![]() .
.
故f(x)的单调递减区间为(0,![]() ),单调递增区间为(
),单调递增区间为(![]() ,+∞),
,+∞),
综上所述,当a≤0时,函数f(x)在(0,+∞)上为减函数,
当a>0时,f(x)在(0,![]() )上为减函数,在(
)上为减函数,在(![]() ,+∞)为增函数;
,+∞)为增函数;
(2)∵g(x)=(1﹣x)ex,∴g′(x)=﹣xex,
当x∈[﹣1,0)时,g′(x)>0,当x∈(0,1]时,g′(x)<0,
又g(0)=1,g(1)=0,g(﹣1)![]() ,∴当x∈[﹣1,1]时,g(x)的值域为[0,1],
,∴当x∈[﹣1,1]时,g(x)的值域为[0,1],
由(1)可知,①当a≤0时,函数f(x)在(0,e]上为减函数,不满足题意;
②当![]() e,即0<a
e,即0<a![]() 时,函数f(x)在(0,e]上为减函数,不满足题意;
时,函数f(x)在(0,e]上为减函数,不满足题意;
③当0![]() e时,即a
e时,即a![]() 时,函数f(x)在区间(0,
时,函数f(x)在区间(0,![]() )上为减函数,在(
)上为减函数,在(![]() ,e]上为增函数,
,e]上为增函数,
又x>0,且x→0时,f(x)→+∞,函数f(x)的大概图像如下图,
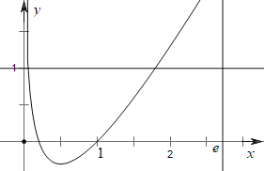
故对任意给定的x0∈[﹣1,1],在区间(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,
当且仅当a满足以下条件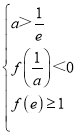 ,即
,即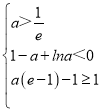 (*)
(*)
令h(a)=1﹣a+lna,a∈(![]() ,+∞),则h′(a)=﹣1
,+∞),则h′(a)=﹣1![]() ,
,
当![]() a<1时,h′(a)>0,当a>1时,h′(a)<0,
a<1时,h′(a)>0,当a>1时,h′(a)<0,
∴函数h(a)在(![]() ,1)上为增函数,在(1,+∞)上为减函数,故h(a)max=h(1)=0,
,1)上为增函数,在(1,+∞)上为减函数,故h(a)max=h(1)=0,
从而(*)等价于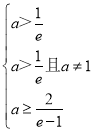 ,故a
,故a![]() ,故a的取值范围为[
,故a的取值范围为[![]() ,+∞).
,+∞).

【题目】世界互联网大会是由中国倡导并每年在浙江省嘉兴市桐乡乌镇举办的世界性互联网盛会,大会旨在搭建中国与世界互联互通的国际平台和国际互联网共享共治的中国平台,让各国在争议中求共识在共识中谋合作在合作中创共赢.2019年10月20日至22日,第六届世界互联网大会如期举行,为了大会顺利召开,组委会特招募了1 000名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15,并根据调查结果画出如图所示的频率分布直方图:
岁内的人数为15,并根据调查结果画出如图所示的频率分布直方图:
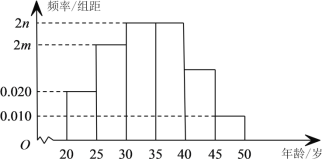
(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)这次大会志愿者主要通过现场报名和登录大会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能
否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: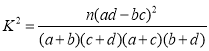 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】学生考试中答对但得不了满分的原因多为答题不规范,具体表现为:解题结果正确,无明显推理错误,但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等,记此类解答为“![]() 类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“
类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“![]() 类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
教师评分(满分12分) | 11 | 10 | 9 |
各分数所占比例 |
|
|
|
某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两名老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于等于1分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于1分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分;当一、二评分数和仲裁分数差值的绝对值相同时,取仲裁分数和前两评中较高的分数的平均分为该题得分.(假设本次考试阅卷老师对满分为12分的题目中的“![]() 类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
(1)本次数学考试中甲同学某题(满分12分)的解答属于“![]() 类解答”,求甲同学此题得分
类解答”,求甲同学此题得分![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)本次数学考试有6个解答题,每题满分均为12分,同学乙6个题的解答均为“![]() 类解答”,记该同学6个题中得分为
类解答”,记该同学6个题中得分为![]() 的题目个数为
的题目个数为![]() ,
,![]() ,
,![]() ,计算事件“
,计算事件“![]() ”的概率.
”的概率.
