题目内容
11.研究下列函数的连续性,并画出函数的图形.(1)f(x)=$\left\{\begin{array}{l}{{x}^{2},0≤x≤1}\\{2-x,1<x≤2}\end{array}\right.$;
(2)f(x)=$\left\{\begin{array}{l}{x,-1≤x≤1}\\{1,x<-1或x>1}\end{array}\right.$.
分析 作出函数的图象,从而确定函数的连续性.
解答 解:(1)作函数f(x)=$\left\{\begin{array}{l}{{x}^{2},0≤x≤1}\\{2-x,1<x≤2}\end{array}\right.$的图象如下,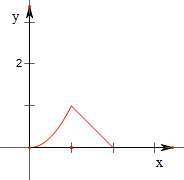
故函数在其定义域上连续;
(2)作函数f(x)=$\left\{\begin{array}{l}{x,-1≤x≤1}\\{1,x<-1或x>1}\end{array}\right.$的图象如下,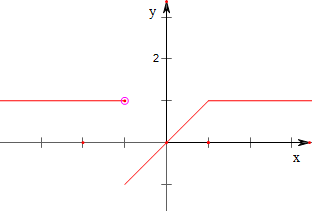
故函数在其定义域上不连续.
点评 本题考查了学生作图的能力及函数的连续性的判断.

练习册系列答案
相关题目
6.函数f(x)=$\left\{\begin{array}{l}{\frac{ln(x+1)}{x-1}\\;x>1}\\{tan\frac{π}{2}x\\;0≤x<1}\\{x+sinx\\;x<0}\end{array}\right.$的全体连续点的集合是( )
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,1)∪(1,+∞) | D. | (-∞,0)∪(0,1)∪(1,+∞) |
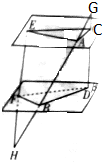 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.