题目内容
已知函数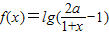 (其中a>0).求证:
(其中a>0).求证:(1)用反证法证明函数f(x)不能为偶函数;
(2)函数f(x)为奇函数的充要条件是a=1.
【答案】分析:(1)假设函数f(x)为偶函数,则f(-x)=f(x),代入利用对数的性质,可得矛盾,即可得证;
(2)分充分性、必要性进行论证,即可得到结论.
解答:证明:(1)假设函数f(x)为偶函数,则f(-x)=f(x),
∴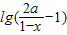 =
=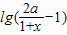 ,即
,即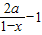 =
=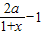 ,化简得:
,化简得: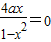 ,
,
∴a=0,与条件a>0矛盾,
∴函数f(x)不能为偶函数.…(7分)
(2)充分性:由a=1,函数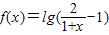 =
=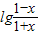 ,
,
∵ >0,∴-1<x<1,
>0,∴-1<x<1,
又f(x)+f(-x)= +
+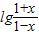 =lg1=0,
=lg1=0,
∴当a=1时,函数f(x)为奇函数.…(10分)
必要性:由函数f(x)为奇函数,即f(x)+f(-x)=0,
∴f(x)+f(-x)=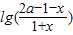 +
+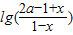 =0,化简得(2a-1)2=1,
=0,化简得(2a-1)2=1,
∵a>0,∴a=1,
∴当函数f(x)为奇函数时,a=1.…(14分)
(注:必要性的证明也可由定义域的对称性得到a=1)
点评:本题考查反证法,考查充要性的证明,考查学生分析解决问题的能力,属于中档题.
(2)分充分性、必要性进行论证,即可得到结论.
解答:证明:(1)假设函数f(x)为偶函数,则f(-x)=f(x),
∴
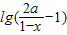 =
=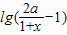 ,即
,即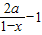 =
=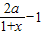 ,化简得:
,化简得: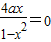 ,
,∴a=0,与条件a>0矛盾,
∴函数f(x)不能为偶函数.…(7分)
(2)充分性:由a=1,函数
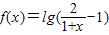 =
=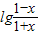 ,
,∵
 >0,∴-1<x<1,
>0,∴-1<x<1,又f(x)+f(-x)=
 +
+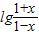 =lg1=0,
=lg1=0,∴当a=1时,函数f(x)为奇函数.…(10分)
必要性:由函数f(x)为奇函数,即f(x)+f(-x)=0,
∴f(x)+f(-x)=
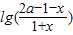 +
+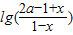 =0,化简得(2a-1)2=1,
=0,化简得(2a-1)2=1,∵a>0,∴a=1,
∴当函数f(x)为奇函数时,a=1.…(14分)
(注:必要性的证明也可由定义域的对称性得到a=1)
点评:本题考查反证法,考查充要性的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.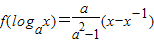 ,其中a>0且a≠1.
,其中a>0且a≠1.