题目内容
已知函数 与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).
与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).(1)求a的值
(2)求F(x)在区间[1,e]上的最小值.
【答案】分析:(1)因为函数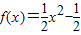 与函数g(x)=alnx在点(1,0)处有公共的切线,且f(1)=g(1)=0,说明点(1,0)在两条曲线上,把两函数求导后根据在(1,0)处的导数值相等可得a的值;
与函数g(x)=alnx在点(1,0)处有公共的切线,且f(1)=g(1)=0,说明点(1,0)在两条曲线上,把两函数求导后根据在(1,0)处的导数值相等可得a的值;
(2)把f(x)与g(x)代入函数F(x)的解析式,然后求其导函数,分m<0和m>0判断导函数的单调性,根据函数的单调性求得F(x)在区间[1,e]上的最小值.其中当m>0时需要由导函数的零点对区间[1,e]进行分段.
解答:解:(1)因为f(1)=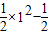 =0,g(1)=aln1=0,所以(1,0)在函数f(x),g(x)的图象上
=0,g(1)=aln1=0,所以(1,0)在函数f(x),g(x)的图象上
又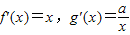 ,所以f'(1)=1,g'(1)=a
,所以f'(1)=1,g'(1)=a
所以a=1
(2)因为F(x)=f(x)-mg(x),所以,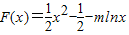 ,其定义域为{x|x>0}
,其定义域为{x|x>0}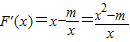
当m<0时, ,
,
所以F(x)在(0,+∞)上单调递增
所以F(x)在[1,e]上单调递增,其最小值为F(1)=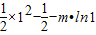 =0.
=0.
当m>0时,令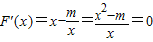 ,得到
,得到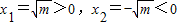 (舍)
(舍)
当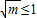 时,即0<m≤1时,F'(x)>0对(1,e)恒成立,
时,即0<m≤1时,F'(x)>0对(1,e)恒成立,
所以F(x)在[1,e]上单调递增,其最小值为F(1)=0
当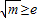 时,即m≥e2时,F'(x)<0对(1,e)成立,
时,即m≥e2时,F'(x)<0对(1,e)成立,
所以F(x)在[1,e]上单调递减,
其最小值为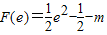
当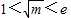 ,即1<m<e2时,F'(x)<0对
,即1<m<e2时,F'(x)<0对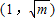 成立,F'(x)>0对
成立,F'(x)>0对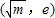 成立
成立
所以F(x)在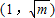 单调递减,在
单调递减,在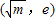 上单调递增
上单调递增
其最小值为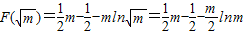 .
.
综上,当m≤1时,F(x)在[1,e]上的最小值为F(1)=0.
当1<m<e2时,F(x)在[1,e]上的最小值为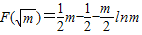 .
.
当m≥e2时,F(x)在[1,e]上的最小值为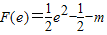 .
.
点评:本题考查了利用导数研究曲线上某点的切线方程,考查了利用导数求函数在闭区间上的最值,求函数在闭区间上的最值,需要求函数在对应开区间上的极值与区间端点的函数值,然后进行大小比较.此题属中档题.
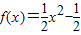 与函数g(x)=alnx在点(1,0)处有公共的切线,且f(1)=g(1)=0,说明点(1,0)在两条曲线上,把两函数求导后根据在(1,0)处的导数值相等可得a的值;
与函数g(x)=alnx在点(1,0)处有公共的切线,且f(1)=g(1)=0,说明点(1,0)在两条曲线上,把两函数求导后根据在(1,0)处的导数值相等可得a的值;(2)把f(x)与g(x)代入函数F(x)的解析式,然后求其导函数,分m<0和m>0判断导函数的单调性,根据函数的单调性求得F(x)在区间[1,e]上的最小值.其中当m>0时需要由导函数的零点对区间[1,e]进行分段.
解答:解:(1)因为f(1)=
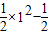 =0,g(1)=aln1=0,所以(1,0)在函数f(x),g(x)的图象上
=0,g(1)=aln1=0,所以(1,0)在函数f(x),g(x)的图象上又
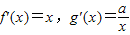 ,所以f'(1)=1,g'(1)=a
,所以f'(1)=1,g'(1)=a所以a=1
(2)因为F(x)=f(x)-mg(x),所以,
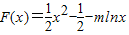 ,其定义域为{x|x>0}
,其定义域为{x|x>0}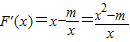
当m<0时,
 ,
,所以F(x)在(0,+∞)上单调递增
所以F(x)在[1,e]上单调递增,其最小值为F(1)=
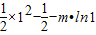 =0.
=0.当m>0时,令
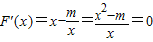 ,得到
,得到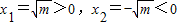 (舍)
(舍)当
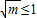 时,即0<m≤1时,F'(x)>0对(1,e)恒成立,
时,即0<m≤1时,F'(x)>0对(1,e)恒成立,所以F(x)在[1,e]上单调递增,其最小值为F(1)=0
当
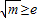 时,即m≥e2时,F'(x)<0对(1,e)成立,
时,即m≥e2时,F'(x)<0对(1,e)成立,所以F(x)在[1,e]上单调递减,
其最小值为
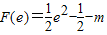
当
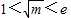 ,即1<m<e2时,F'(x)<0对
,即1<m<e2时,F'(x)<0对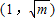 成立,F'(x)>0对
成立,F'(x)>0对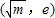 成立
成立所以F(x)在
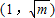 单调递减,在
单调递减,在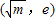 上单调递增
上单调递增其最小值为
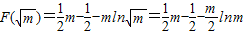 .
.综上,当m≤1时,F(x)在[1,e]上的最小值为F(1)=0.
当1<m<e2时,F(x)在[1,e]上的最小值为
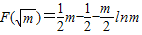 .
.当m≥e2时,F(x)在[1,e]上的最小值为
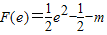 .
.点评:本题考查了利用导数研究曲线上某点的切线方程,考查了利用导数求函数在闭区间上的最值,求函数在闭区间上的最值,需要求函数在对应开区间上的极值与区间端点的函数值,然后进行大小比较.此题属中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称, 的最大值为
的最大值为  =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 . 与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).
与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).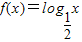 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,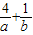 的最大值为
的最大值为 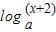 =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .