题目内容
已知函数 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,(1)若g(a)g(b)=2,且a<0,b<0,则
 的最大值为
的最大值为 (2)设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2-x)=f(x+2),且当x∈[-2,0]时,f(x)=g(x)-1,若关于x的方程f(x)-
 =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
【答案】分析:(1)根据题意,由反函数的定义以及对数函数、指数函数的性质可得g(x)=( )x=2-x,进而结合题意可得2-(a+b)=2,即a+b=-1,对
)x=2-x,进而结合题意可得2-(a+b)=2,即a+b=-1,对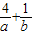 变形可得其等于-[5+
变形可得其等于-[5+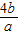 +
+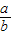 ],由基本不等式的性质可得
],由基本不等式的性质可得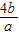 +
+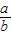 ≥4,代入
≥4,代入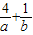 =-[5+
=-[5+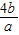 +
+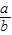 ]可得其最大值,即可得答案.
]可得其最大值,即可得答案.
(2)根据题意,分析可得函数f(x)是一个周期函数,且周期为4,将方程f(x)-logax+2=0恰有3个不同的实数解,转化为函数f(x)的与函数y=-logax+2的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
解答:解:(1)根据题意,g(x)=( )x=2-x,
)x=2-x,
若g(a)g(b)=2,则有2-(a+b)=2,即a+b=-1,
则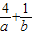 =-[(-a)+(-b)][
=-[(-a)+(-b)][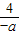 +
+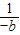 ]=-[5+
]=-[5+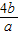 +
+ ],
],
又由a<0,b<0,则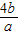 >0且
>0且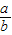 >0,故
>0,故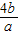 +
+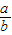 ≥4,
≥4,
则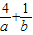 =-[5+
=-[5+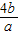 +
+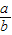 ]≤-9,
]≤-9,
即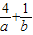 的最大值为-9;
的最大值为-9;
(2)对于任意的x∈R,都有f(x-2)=f(2+x),∴函数f(x)是一个周期函数,且T=4.
又∵当x∈[-2,0]时,f(x)=( )x-1,且函数f(x)是定义在R上的偶函数,
)x-1,且函数f(x)是定义在R上的偶函数,
若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=-loga(x+2)在区间(-2,6]上有三个不同的交点,
又f(-2)=f(2)=3,分析可得有 loga4<3,且loga8>3,解得: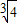 <a<2,
<a<2,
则a的取值范围是(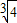 ,2)
,2)
故答案为(1):-9;(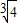 ,2).
,2).
点评:本题考查指数函数与对数函数的图象与性质,以及基本不等式的应用,(1)的关键是根据题意,求出g(x)的解析式,其次要注意题意中a<0,b<0的条件,要配凑基本不等式成立的条件.
 )x=2-x,进而结合题意可得2-(a+b)=2,即a+b=-1,对
)x=2-x,进而结合题意可得2-(a+b)=2,即a+b=-1,对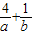 变形可得其等于-[5+
变形可得其等于-[5+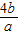 +
+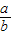 ],由基本不等式的性质可得
],由基本不等式的性质可得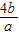 +
+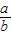 ≥4,代入
≥4,代入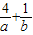 =-[5+
=-[5+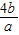 +
+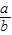 ]可得其最大值,即可得答案.
]可得其最大值,即可得答案.(2)根据题意,分析可得函数f(x)是一个周期函数,且周期为4,将方程f(x)-logax+2=0恰有3个不同的实数解,转化为函数f(x)的与函数y=-logax+2的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
解答:解:(1)根据题意,g(x)=(
 )x=2-x,
)x=2-x,若g(a)g(b)=2,则有2-(a+b)=2,即a+b=-1,
则
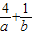 =-[(-a)+(-b)][
=-[(-a)+(-b)][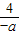 +
+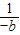 ]=-[5+
]=-[5+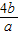 +
+ ],
],又由a<0,b<0,则
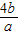 >0且
>0且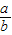 >0,故
>0,故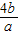 +
+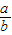 ≥4,
≥4,则
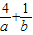 =-[5+
=-[5+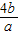 +
+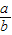 ]≤-9,
]≤-9,即
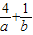 的最大值为-9;
的最大值为-9;(2)对于任意的x∈R,都有f(x-2)=f(2+x),∴函数f(x)是一个周期函数,且T=4.
又∵当x∈[-2,0]时,f(x)=(
 )x-1,且函数f(x)是定义在R上的偶函数,
)x-1,且函数f(x)是定义在R上的偶函数,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=-loga(x+2)在区间(-2,6]上有三个不同的交点,
又f(-2)=f(2)=3,分析可得有 loga4<3,且loga8>3,解得:
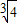 <a<2,
<a<2,则a的取值范围是(
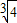 ,2)
,2)故答案为(1):-9;(
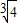 ,2).
,2).点评:本题考查指数函数与对数函数的图象与性质,以及基本不等式的应用,(1)的关键是根据题意,求出g(x)的解析式,其次要注意题意中a<0,b<0的条件,要配凑基本不等式成立的条件.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).
与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).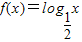 与函数g(x)的图象关于y=x对称,
与函数g(x)的图象关于y=x对称,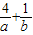 的最大值为
的最大值为 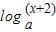 =0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 .
=0(a>1)在区间(-2,6]内恰有三个不同实根,则实数a的取值范围是 . 与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).
与函数g(x)=alnx在点(1,0)处有公共的切线,设F(x)=f(x)-mg(x)(m≠0).