题目内容
已知曲线y=2sin(x+
)cos(
-x)与直线y=
相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3,…,则|P1P2|=( )
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
分析:将y=2sin(x+
)cos(
-x)化为y=1+sin2x,求出方程的解x,即可求解|P1P2|,从而可得答案.
| π |
| 4 |
| π |
| 4 |
解答:解:∵x+
+(
-x)=
,
∴y=2sin(x+
)cos(
-x)
=2cos2(
-x)
=1+cos(
-2x)
=1+sin2x,
∴1+sin2x=
,
可得sin2x=-
,
∴x=kπ+
,或x=kπ+
,k∈Z.|P1P2|=|
-
|=
.
故选:C.
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴y=2sin(x+
| π |
| 4 |
| π |
| 4 |
=2cos2(
| π |
| 4 |
=1+cos(
| π |
| 2 |
=1+sin2x,
∴1+sin2x=
| 1 |
| 2 |
可得sin2x=-
| 1 |
| 2 |
∴x=kπ+
| 7π |
| 12 |
| 11π |
| 12 |
| 11π |
| 12 |
| 7π |
| 12 |
| π |
| 3 |
故选:C.
点评:本题考查三角函数中的恒等变换应用,考查三角函数二倍角公式的应用,方程的解法,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 )cos(
)cos(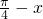 )与直线y=
)与直线y= 相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3,…,则|
相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3,…,则|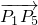 |等于
|等于