题目内容
已知曲线y=2sin(x+
)cos（
-x）与直线y=
相交，若在y轴右侧的交点自左向右依次记为P1，P2，P3，…，则|
|等于（ ）
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| p3p5 |
分析：将y=2sin(x+
)cos（
-x）化为y=1+sin2x，可求得其周期，作出其图象，可知|
|=T，从而可得答案．
| π |
| 4 |
| π |
| 4 |
| p3p5 |
解答：解：∵x+
+（
-x）=
，
∴y=2sin(x+
)cos（
-x）
=2cos2(
-x)
=1+cos（
-2x）
=1+sin2x，其图象如下，
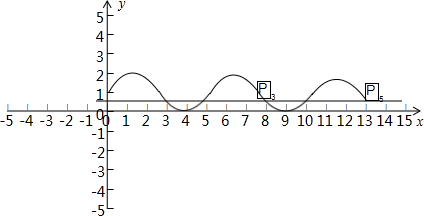
由图象可知，|
|=T=
=π，
故选A．
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴y=2sin(x+
| π |
| 4 |
| π |
| 4 |
=2cos2(
| π |
| 4 |
=1+cos（
| π |
| 2 |
=1+sin2x，其图象如下，
由图象可知，|
| p3p5 |
| 2π |
| 2 |
故选A．
点评：本题考查三角函数中的恒等变换应用，考查三角函数的周期性及其求法，考查作图与理解应用的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
）cos（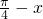
）与直线y=
相交，若在y轴右侧的交点自左向右依次记为P1，P2，P3，…，则|
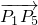|等于