题目内容
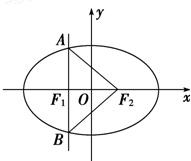
F1、F2分别为椭圆
的左、右焦点，A为短轴一端点，弦AB过左焦点F1，则△ABF2的面积为（ ）A．
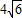
B．
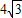
C．3
D．4
【答案】分析：设A（0，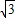
），得直线AF1方程为y=x+
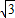，与椭圆
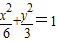消去x得3y2-2
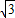y-3=0，从而得到yA=
，yB=-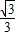
．而△ABF2的面积S=
|F1F2|•|yA-yB|，因此算出椭圆的焦距，再代入前面算出的数据，即得所求△ABF2的面积．
解答：解：∵椭圆方程是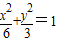
，∴椭圆的左焦点F1（-
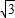，0），右焦点F2（
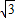，0）
设A为上端点，得A（0，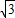
），求得AF1的斜率k=1，得直线AF1的方程为y=x+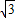
将直线AF1的方程与椭圆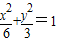
消去x，得3y2-2
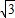y-3=0
解之可得yA=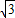
，yB=-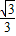
∵椭圆的焦距|F1F2|=2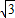
∴△ABF2的面积S=
|F1F2|•|yA-yB|=
•2
•
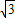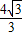=4
故选：D
点评：本题给出椭圆经过左焦点和短轴一端的内接三角形，求此三角形的面积，着重考查了椭圆的标准方程与简单几何性质、直线与椭圆位置关系等知识，属于中档题．
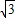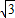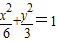），得直线AF1方程为y=x+，与椭圆消去x得3y2-2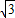y-3=0，从而得到yA=，yB=-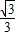．而△ABF2的面积S=|F1F2|•|yA-yB|，因此算出椭圆的焦距，再代入前面算出的数据，即得所求△ABF2的面积．解答：解：∵椭圆方程是
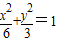，∴椭圆的左焦点F1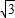（-，0），右焦点F2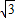（，0）设A为上端点，得A（0，
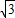），求得AF1的斜率k=1，得直线AF1的方程为y=x+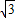将直线AF1的方程与椭圆
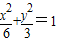消去x，得3y2-2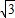y-3=0解之可得yA=
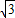，yB=-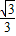∵椭圆的焦距|F1F2|=2
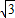
∴△ABF2的面积S=
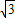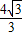|F1F2|•|yA-yB|=•2•=4故选：D
点评：本题给出椭圆经过左焦点和短轴一端的内接三角形，求此三角形的面积，着重考查了椭圆的标准方程与简单几何性质、直线与椭圆位置关系等知识，属于中档题．
练习册系列答案
相关题目
已知F1，F2分别为椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
A、（0，
| ||
B、（0，
| ||
C、（
| ||
D、（
|
（2012•鹰潭一模）已知椭圆