题目内容
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
【答案】
(Ⅰ)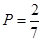
(Ⅱ)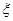 的分布列为
的分布列为
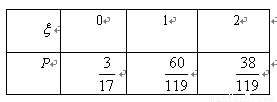 ;
;
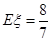
【解析】(Ⅰ)从50名教师随机选出2名的方法数为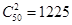 ,
,
选出2人使用版本相同的方法数为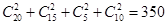 ,
,
故2人使用版本相同的概率为: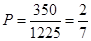 。……6分
。……6分
(Ⅱ)∵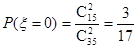 ,
,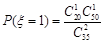 ,
, 。
。
∴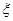 的分布列为
的分布列为

……12分
∴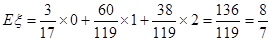 。……14分
。……14分

练习册系列答案
相关题目
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为ξ,求随机变量ξ的变分布列和数学期望.
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 5 | 10 |
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为ξ,求随机变量ξ的变分布列和数学期望.
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 5 | 10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望。
的分布列和数学期望。
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为ξ,求随机变量ξ的分布列.
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为ξ,求随机变量ξ的变分布列和数学期望.
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 5 | 10 |
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为ξ,求随机变量ξ的变分布列和数学期望.