题目内容
已知曲线f(x)=x2+2x在点(x1,f(x1))处的切线为l.
(Ⅰ)求l的方程;
(Ⅱ)设g(x)=(x+a)f(x),若g(x)在[1,2]上是增函数,求实数a的取值范围;
(Ⅲ)试判断l能否与曲线g(x)=ln(x+1)相切?并说明理由.
答案:
解析:
解析:
|
(文科) (1) ∴ (2)∵ ∴ ∵ 于是 ∴ (理科) (1) ∴ (2)设曲线 其切线方程为 欲使此切线与 即需要判断关于 由(1)式中的 设 ∴ 所以 |

练习册系列答案
相关题目
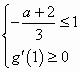 ,或
,或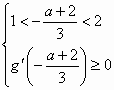 ,或
,或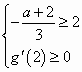 解得
解得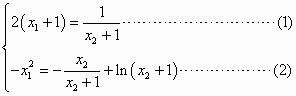 ,
,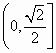 ,增区间是
,增区间是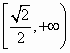 ,故
,故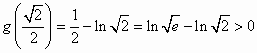
 ,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直. ax2+3x.
ax2+3x. ax2+3x.
ax2+3x.