题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),过点B(0,b)作圆x2+y2=$\frac{{b}^{2}}{4}$的两条切线BM、BN,切点分别为点M和N,若$\overrightarrow{BM}$•$\overrightarrow{BN}$=$\frac{3}{8}$,且该椭圆的离心率为$\frac{\sqrt{2}}{2}$,点O为坐标原点.(Ⅰ)求椭圆C的方程;
(Ⅱ)点F1、F2分别是椭圆C的左右焦点,四个顶点都在椭圆C上的平行四边形PQIJ的两条对边PQ、IJ分别经过点F1、F2,求平行四边形PQIJ面积的最大值.
分析 (Ⅰ)由题意∠MBN=60°,BM=BN=$\frac{\sqrt{3}}{2}$b,利用$\overrightarrow{BM}$•$\overrightarrow{BN}$=$\frac{3}{8}$,求出b,椭圆的离心率为$\frac{\sqrt{2}}{2}$,可得a,c,即可求椭圆C的方程;
(Ⅱ)由题意,平行四边形PQIJ面积最大时,平行四边形PQIJ为矩形,即可得出结论.
解答 解:(Ⅰ)由题意∠MBN=60°,BM=BN=$\frac{\sqrt{3}}{2}$b,
∵$\overrightarrow{BM}$•$\overrightarrow{BN}$=$\frac{3}{8}$,
∴$\frac{3}{4}{b}^{2}•\frac{1}{2}$=$\frac{3}{8}$,
∴b=1,
∵椭圆的离心率为$\frac{\sqrt{2}}{2}$,
∴$\frac{c}{a}=\frac{\sqrt{2}}{2}$,
∴c=1,a=$\sqrt{2}$,
∴椭圆C的方程是$\frac{{x}^{2}}{2}+{y}^{2}$=1由题意;
(Ⅱ)由题意,平行四边形PQIJ面积最大时,平行四边形PQIJ为矩形,
∵x=1时,y=$\frac{\sqrt{2}}{2}$,
∴平行四边形PQIJ面积的最大值为2$\sqrt{2}$.
点评 本题考查椭圆的方程与性质,考查向量知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若存在非零实数x,y,使不等式(6a-1)x2-2xy+ay2≥0成立,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (-∞-$\frac{1}{3}$)∪($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{3}$,+∞) | D. | [$\frac{1}{2}$,+∞) |
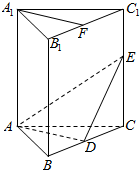 如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,F为B1C1的中点,D,E分别是棱BC,CC1上的点,且AD⊥BC.
如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,F为B1C1的中点,D,E分别是棱BC,CC1上的点,且AD⊥BC.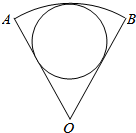 如图所示:“十字形”公路的交叉处周围呈扇形形状,某市规划拟在这块扇形土尘修建一个圆形广扬,已知∠A0B=60°,AB的长度=100πm,怎样设计广场的占地面积最大?其值是多少?
如图所示:“十字形”公路的交叉处周围呈扇形形状,某市规划拟在这块扇形土尘修建一个圆形广扬,已知∠A0B=60°,AB的长度=100πm,怎样设计广场的占地面积最大?其值是多少?