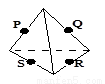Question

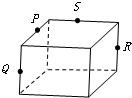
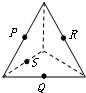
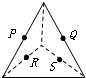
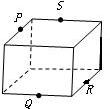
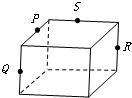
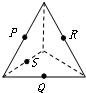
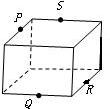
2、下列各图中P、Q、R、S分别是各棱的中点，其中四个点不共面的图是（　　）

A、

B、

C、

D、

Answer 1

分析：由中点构成的中位线和几何体的特征先判断是否平行，再判断是否在同一个平面内．

解答：解：A、有题意和长方体知，PS∥QR，则P、Q、R、S四个点共面，故A不对；
B、根据图中几何体得，P、Q、R、S四个点中任意两个点都在两个平面内，并且任意两个点的连线既不平行也不相交，故四个点共面不共面，故B正确；
C、因PR和QS分别是相邻侧面的中位线，所以PR∥QS，即P、Q、R、S四个点共面，故C不对；
D、有题意和长方体知，PS∥QR，则P、Q、R、S四个点共面，故D不对；
故选B．

点评：本题考查了公理2以及推论的应用，主要根据中点构成中位线的性质和几何体进行判断．