题目内容
给出下列命题:①命题“?x∈R,使得x2+x+1<0”的非命题是“对?x∈R,都有x2+x+1>0”;
②独立性检验显示“患慢性气管炎和吸烟有关”,这就是“有吸烟习惯的人,必定会患慢性气管炎”;
③某校有高一学生300人,高二学生270人,高三学生210人,现教育局欲用分层抽样的方法,抽取26名学生进行问卷调查,则高三学生被抽到的概率最小.
其中错误的命题序号是
分析:据特称命题的否定是全称命题:将存在改为任意,结论否定;得到①错误;
独立性检验显示的分类变量有关、无关不是确定关系,故两个分类变量有关时,不能推出一个存在另一个一定存在故②错;
在抽样方法中,每种抽样方法都遵循每个个体被抽到的概率相等的特点,故③错.
独立性检验显示的分类变量有关、无关不是确定关系,故两个分类变量有关时,不能推出一个存在另一个一定存在故②错;
在抽样方法中,每种抽样方法都遵循每个个体被抽到的概率相等的特点,故③错.
解答:解:①中原命题的非命题是“对?x∈R,都有x2+x+1≥0”,所以①错误;
②中说法不正确,“患慢性气管炎和吸烟有关”只是说明“患慢性气管炎”和“吸烟”有一定的相关关系,但不是确定关系,所以“有吸烟习惯的人,未必患慢性气管炎”;
③中,由于抽样比为
=
,所以高一学生被抽到的人数为
×300=10人,高二学生被抽到的人数为
×270=9人,高三学生被抽到的人数为
×210=7人,尽管高三学生抽到的人数少,但每个学生被抽到的机会均等,所以“高三学生被抽到的概率最小”这种说法错误.
故答案为①②③
②中说法不正确,“患慢性气管炎和吸烟有关”只是说明“患慢性气管炎”和“吸烟”有一定的相关关系,但不是确定关系,所以“有吸烟习惯的人,未必患慢性气管炎”;
③中,由于抽样比为
| 26 |
| 300+270+210 |
| 1 |
| 30 |
| 1 |
| 30 |
| 1 |
| 30 |
| 1 |
| 30 |
故答案为①②③
点评:本题三个命题重点考查简易逻辑用语、统计案例和统计等基本概念.

练习册系列答案
相关题目
 y =
y = 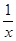 的一个交点;
的一个交点; 的一个交点
的一个交点 的一个交点
的一个交点 (
( 的一个交点;
的一个交点; 的一个交点;
的一个交点; 的一个交点;
的一个交点; (
(