题目内容
已知函数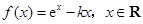
(Ⅰ)若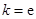 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若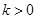 ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数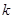 的取值范围;
的取值范围;
(Ⅲ)设函数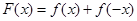 ,求证:
,求证: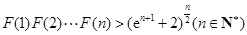 .
.
【答案】
(1)增区间是 ,减区间是
,减区间是
(2)
(3)构造函数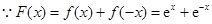 ,
,

 ,
,
则放缩法得到证明。
【解析】
试题分析:解:(Ⅰ)由 得
得 ,所以
,所以 .
.
由 得
得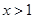 ,故
,故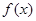 的单调递增区间是
的单调递增区间是 ,
,
由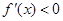 得
得 ,故
,故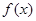 的单调递减区间是
的单调递减区间是 .
.
(Ⅱ)由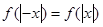 可知
可知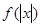 是偶函数.
是偶函数.
于是 对任意
对任意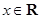 成立等价于
成立等价于 对任意
对任意 成立.
成立.
由 得
得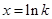 .
.
①当 时,
时,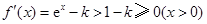 .
.
此时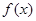 在
在 上单调递增.故
上单调递增.故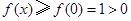 ,符合题意.
,符合题意.
②当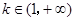 时,
时, .
.
当 变化时
变化时 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
单调递减 |
极小值 |
单调递增 |
由此可得,在 上,
上, .
.
依题意, ,又
,又 .
.
综合①,②得,实数 的取值范围是
的取值范围是 .
.
(Ⅲ)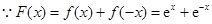 ,
,

 ,
,
 ,
,
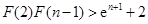
…….

由此得,
故 .
.
考点:导数的运用
点评:解决的关键是对于函数单调性的判定以及运用函数的极值来得到参数的 范围,属于中档题。

练习册系列答案
相关题目






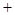
 ,
, 
 .
. , 函数
, 函数 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围; 的最小值;
的最小值; 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 ,问是否存在点
,问是否存在点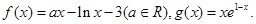
 图象在(0,0)处的切线也恰为
图象在(0,0)处的切线也恰为 图象的一条切线,求实数a的值;
图象的一条切线,求实数a的值; ,都有唯一的
,都有唯一的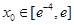 ,使得
,使得 成立,若存在,求出a的取值范围;若不存在,请说明理由。
成立,若存在,求出a的取值范围;若不存在,请说明理由。
 ,求
,求 的单调递减区间;
的单调递减区间; ,求
,求 的最小值;
的最小值; ,且存在
,且存在 使得
使得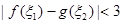 ,求实数
,求实数 的取值范围。
的取值范围。 .
. ,求函数
,求函数 在区间
在区间 的值域;
的值域; 上为增函数,求
上为增函数,求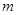 的取值范围.
的取值范围.