题目内容
已知a<b函数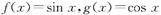 ,若命题
,若命题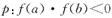 ,命题q:g(x)在 (a,b) 内有最值,则命题p是命题q成立的( )
,命题q:g(x)在 (a,b) 内有最值,则命题p是命题q成立的( )
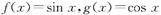 ,若命题
,若命题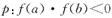 ,命题q:g(x)在 (a,b) 内有最值,则命题p是命题q成立的( )
,命题q:g(x)在 (a,b) 内有最值,则命题p是命题q成立的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
试题分析:∵f(a)•f(b)<0,
又∵f(x)在R上连续
根据函数的零点判定定理可知,函数f(x)在(a,b)上存在零点
根据正弦函数、余弦函数的性质可知,正弦函数的零点是余弦函数的最值点
∴g(x)=cosx在(a,b)上有最值,∴p⇒q
若g(x)=cosx在(a,b)上有最值则根据余弦函数的零点是正弦函数的零点
则f(x)=sinx在(a,b)上有零点,但是由于函数f(x)=sinx在(a,b)不一定单调,f(a)f(b)<0不一定成立
故命题p:f(a)•f(b)<0,命题q:函数g(x)在区间(a,b)内有最值的充分不必要条件,故选A
点评:解题的关键是准确、熟练的应用函数的零点定理及正弦函数与余弦函数的性质分析和解决问题。由f(a)•f(b)<0,及f(x)在R上连续可知函数f(x)在(a,b)上存在零点,然后结合正弦函数的零点是余弦函数的最值点可判断,若g(x)=cosx在(a,b)上有最值,f(x)=sinx在(a,b)上有零点,但由于函数f(x)=sinx在(a,b)不一定单调,f(a)f(b)<0不一定成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
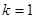 ”是“直线
”是“直线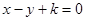 与圆
与圆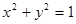 相交”的
相交”的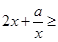 2”的
2”的 :函数
:函数 的定义域为
的定义域为 ;命题
;命题 :不等式
:不等式 对一切正实数均成立.如果命题“
对一切正实数均成立.如果命题“ 的取值范围是 ( )
的取值范围是 ( )



 是非空集合,命题甲:
是非空集合,命题甲: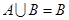 ,命题乙:
,命题乙: ,那么 ( )
,那么 ( )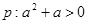 , 条件
, 条件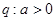 ; 那么
; 那么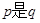 的( )
的( ) ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行的( )
平行的( ) 的公比为
的公比为 ,则“
,则“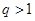 ”是“
”是“ ”的既不充分也不必要条件;(2)“
”的既不充分也不必要条件;(2)“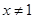 ”是“
”是“ ”的必要不充分条件;(3)函数的
”的必要不充分条件;(3)函数的 的值域为R,则实数
的值域为R,则实数 ;(4)“
;(4)“ ”是“函数
”是“函数 的最小正周期为
的最小正周期为 ”的充要条件.其中真命题的个数是
”的充要条件.其中真命题的个数是 ,
, ,满足
,满足 ,
, ,则 “
,则 “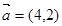 ”是 “
”是 “