题目内容
设 为数列
为数列 的前
的前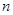 项和,对任意的
项和,对任意的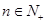 ,都有
,都有 (
(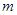 为正常数).
为正常数).
(1)求证:数列 是等比数列;
是等比数列;
(2)数列 满足
满足 求数列
求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前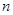 项和
项和 .
.
(1)证明详见解析;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)利用 求出
求出 与
与 的关系,判断数列是等差数列,从而写出等差数列的通项公式;(2)因为
的关系,判断数列是等差数列,从而写出等差数列的通项公式;(2)因为 ,所以可以证明
,所以可以证明 是首项为
是首项为 ,公差为1的等差数列,先求出
,公差为1的等差数列,先求出 的通项公式,再求
的通项公式,再求 ;(3)把第(2)问的
;(3)把第(2)问的 代入,利用错位相减法求
代入,利用错位相减法求 .
.
试题解析:(1)证明:当 时,
时, ,解得
,解得 . 1分
. 1分
当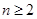 时,
时, .即
.即 . 2分
. 2分
又 为常数,且
为常数,且 ,∴
,∴ .
.
∴数列 是首项为1,公比为
是首项为1,公比为 的等比数列.
3分
的等比数列.
3分
(2)解: .
4分
.
4分
∵ ,∴
,∴
 ,即
,即 . 5分
. 5分
∴ 是首项为
是首项为 ,公差为1的等差数列.
6分
,公差为1的等差数列.
6分
∴ ,即
,即 .
7分
.
7分
(3)解:由(2)知 ,则
,则
所以 8分
8分
当 为偶数时,
为偶数时,

令 ①
①
则 ②
②
①-②得 
=
= =
=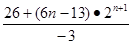
 10分
10分
令 ③
③
 ④
④
③-④得
=
= =
=
 11分
11分

12分
当 为奇数时,
为奇数时, 为偶数,
为偶数,

=
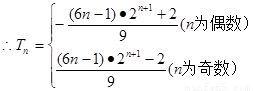 14分
14分
法二: 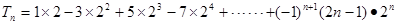 ①
①
 ②
②
9分
①-②得:
 10分
10分
= 12分
12分
=
 13分
13分
∴ 14分
14分
考点:1.等差数列的判定;2.错位相减法求和;3.分类讨论思想.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案 为数列
为数列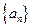 的前
的前 项和,对任意的
项和,对任意的 N
N ,都有
,都有
 为常数,且
为常数,且 .
. ,数列
,数列 满足
满足
 ,
, ,求数列
,求数列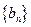 的通项公式;
的通项公式; 的前
的前 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有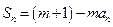
 为常数,且
为常数,且 .
.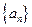 是等比数列;
是等比数列; ,数列
,数列 满足
满足 ,求数列
,求数列 的前
的前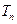 .
. 定义在区间
定义在区间 上,
上, ,且当
,且当 时,
时, .又数列
.又数列 满足
满足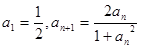 .
. 的表达式;
的表达式; 为数列
为数列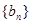 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的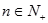 ,都有
,都有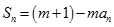
 为常数,且
为常数,且 .
. 是等比数列;
是等比数列; ,数列
,数列 满足
满足 ,求数列
,求数列 的前
的前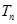 .
.