题目内容
在△ABC中，M是BC的中点，AM=2，BC=5，则
•
= ．
| AB |
| AC |
分析：由条件利可得
•
=（
-
）•（
-
），再利用两个向量的数量积的定义，运算求得结果．
| AB |
| AC |
| MB |
| MA |
| MC |
| MA |
解答：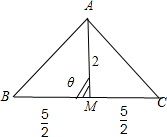
解：如图所示：设∠AMB=θ，则∠AMC=π-θ．
又
=
-
，
=
-
，
∴
•
=（
-
）•（
-
）
=
•
-
•
-
•
+
2
=
×
×cosπ-
×2×cosθ-
×2×cos（π-θ）+22=-
+4=-
，
故答案为-
．
解：如图所示：设∠AMB=θ，则∠AMC=π-θ．又
| AB |
| MB |
| MA |
| AC |
| MC |
| MA |
∴
| AB |
| AC |
| MB |
| MA |
| MC |
| MA |
=
| MB |
| MC |
| MB |
| MA |
| MA |
| MC |
| MA |
=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
| 1 |
| 4 |
故答案为-
| 1 |
| 4 |
点评：本题主要考查两个向量的数量积的定义，两个向量的加减法及其几何意义，属于中档题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
＝2
，则
·（
+ 
）等于
）的图象上每点的横坐标和纵坐标都变为原来的
倍，再把图象向右平移
单位，所得图象解析式为y=2sin（2x-
）
等于-4．
上单调递增，函数f（x）在区间
上单调递减．
）的图象上每点的横坐标和纵坐标都变为原来的
倍，再把图象向右平移
单位，所得图象解析式为y=2sin（2x-
）
等于-4．
上单调递增，函数f（x）在区间
上单调递减．