题目内容
6、[1]函数f（x）=x3+ax2+3x-9，已知f（x）在x=-3时取得极值，则a=
[2]观察下列等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…由此推测第n个等式为
5
．[2]观察下列等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…由此推测第n个等式为
1-4+9-16+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）
．（不必化简结果）分析：[1]先由函数f（x）=x3+ax2+3x-9求出其导函数f′（x），然后根据f′（-3）=0即可求a．
[2]观察等式，发现规律：第n个等式左侧是通项为（-1）n+1n2的前n项和，右侧为（-1）n+1（1+2+3+…+n），则第n个等式即可写出．
[2]观察等式，发现规律：第n个等式左侧是通项为（-1）n+1n2的前n项和，右侧为（-1）n+1（1+2+3+…+n），则第n个等式即可写出．
解答：解：[1]函数f′（x）=3x2+2ax+3，
又f（x）在x=-3时取得极值，
∴f′（-3）=3×9-6a+3=0，解得a=5．
[2]由等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…
可见第n个等式左侧是通项为（-1）n+1n2的前n项和，右侧为（-1）n+1（1+2+3+…+n），
所以第n个等式为 1-4+9-16+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）．
故答案为：[1]5；[2]1-4+9-16+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）．
又f（x）在x=-3时取得极值，
∴f′（-3）=3×9-6a+3=0，解得a=5．
[2]由等式：1=1，1-4=-（1+2），1-4+9=（1+2+3），1-4+9-16=-（1+2+3+4），…
可见第n个等式左侧是通项为（-1）n+1n2的前n项和，右侧为（-1）n+1（1+2+3+…+n），
所以第n个等式为 1-4+9-16+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）．
故答案为：[1]5；[2]1-4+9-16+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）．
点评：函数y=f（x）在x=a时有极值的问题：一般需利用f′（a）=0解决．而观察规律问题是对学生观察能力、归纳推理能力的考查．
练习册系列答案
相关题目
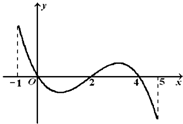
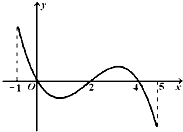已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f'（x）的图象如图所示．下列关于f（x）的命题：