题目内容
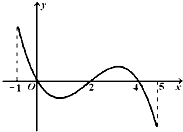已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f'（x）的图象如图所示．下列关于f（x）的命题：| X | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中正确命题的序号是
分析：由导函数的图象得到原函数的单调区间，由此判断命题①②，由定义域和值域的关系判断命题③，结合极小值f（2）的大小判断当1＜a＜2时函数y=f（x）-a的零点情况．
解答：由导函数的图象可知：当x∈（-1，0），（2，4）时，f′（x）＞0，
函数f（x）增区间为（-1，0），（2，4）；
当x∈（0，2），（4，5）时，f′（x）＜0，
函数f（x）减区间为（0，2），（4，5）．
由此可知函数f（x）的极大值点为0，4，命题①正确；
∵函数在x=0，2处有意义，∴函数f（x）在[0，2]上是减函数，命题②正确；
当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为5，命题③不正确；
2是函数的极小值点，若f（2）＞1，则函数y=f（x）-a不一定有4个零点，命题④不正确．
∴正确命题的序号是①②．
故答案为：①②．
函数f（x）增区间为（-1，0），（2，4）；
当x∈（0，2），（4，5）时，f′（x）＜0，
函数f（x）减区间为（0，2），（4，5）．
由此可知函数f（x）的极大值点为0，4，命题①正确；
∵函数在x=0，2处有意义，∴函数f（x）在[0，2]上是减函数，命题②正确；
当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为5，命题③不正确；
2是函数的极小值点，若f（2）＞1，则函数y=f（x）-a不一定有4个零点，命题④不正确．
∴正确命题的序号是①②．
故答案为：①②．
点评：本题主要考查函数的单调性与其导函数的正负之间的关系，考查了函数的极值点两侧函数的单调性，训练了函数的零点与对应图象交点的关系，属中档题．
练习册系列答案
相关题目
