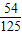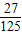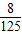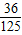题目内容
某人投篮球3次，三次中能中一次的概率为
，能中2次的概率为
，能中3次的概率为
，那么此人三次投篮都不中的概率为（ ）
| 54 |
| 125 |
| 36 |
| 125 |
| 8 |
| 125 |
分析：根据题意，易得“投篮命中”与“三次投篮都不中”为对立事件，而“投篮命中”有3种情况，即“投中1次”、“投中2次”、“投中3次”，依题意，易得“投篮命中”的概率，由对立事件的概率性质，可得答案．
解答：解：根据题意，某人投篮球3次，“投篮命中”有3种情况，即“投中1次”、“投中2次”、“投中3次”，
则“投篮命中”的概率为
+
+
=
，
“投篮命中”与“三次投篮都不中”为对立事件，
则此人三次投篮都不中的概率为1-
=
，
故选B．
则“投篮命中”的概率为
| 54 |
| 125 |
| 36 |
| 125 |
| 8 |
| 125 |
| 98 |
| 125 |
“投篮命中”与“三次投篮都不中”为对立事件，
则此人三次投篮都不中的概率为1-
| 98 |
| 125 |
| 27 |
| 125 |
故选B．
点评：本题考查对立事件的概率性质，注意区分对立事件与互斥事件的不同．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
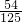，能中2次的概率为
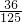，能中3次的概率为
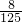，那么此人三次投篮都不中的概率为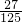
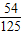，能中2次的概率为
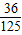，能中3次的概率为
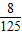，那么此人三次投篮都不中的概率为（ ）
