题目内容
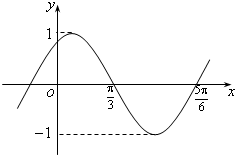（2011•东城区一模）已知函数y=sin（ωx+φ）(ω＞0， 0＜φ≤| π |
| 2 |
分析：由
=
可求T，由T=
可求得ω，由ω•
+φ=π，可求得φ，从而可求得点P（ω，φ）的坐标．
| T |
| 2 |
| π |
| 2 |
| 2π |
| ω |
| π |
| 3 |
解答：解：设其周期为T，由图象可知，
=
-
=
，
∴T=π，
又T=
，∴ω=2，
又∵y=sin（ωx+φ）(ω＞0， 0＜φ≤
)的图象经过（
，0），
∴ω•
+φ=π，解得φ=
；
∴P点的坐标为（2，
）．
故选A．
| T |
| 2 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 2 |
∴T=π，
又T=
| 2π |
| ω |
又∵y=sin（ωx+φ）(ω＞0， 0＜φ≤
| π |
| 2 |
| π |
| 3 |
∴ω•
| π |
| 3 |
| π |
| 3 |
∴P点的坐标为（2，
| π |
| 3 |
故选A．
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，解决的关键是根据图象提供的信息确定ω，φ，考查学生读图的能力与解决问题的能力，属于中档题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
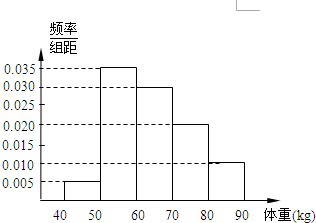（2011•东城区一模）从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．由图中数据可知体重的平均值为