题目内容
已知数列![]() 前n项的和为Sn,且有Sn+1=kSn+2 (n∈N*),a1=2,a2=1.
前n项的和为Sn,且有Sn+1=kSn+2 (n∈N*),a1=2,a2=1.
(1)试证明:数列![]() 是等比数列,并求an;
是等比数列,并求an;
(2)![]() ,不等式
,不等式![]() 恒成立,求正整数t的值;
恒成立,求正整数t的值;
(3)试判断:数列![]() 中任意两项的和在不在数列
中任意两项的和在不在数列![]() 中?请证明你的判断。
中?请证明你的判断。
解:(1)由Sn+1=kSn+2 (n∈N*),a1=2,a2=1,令n=1得k=![]() ………1分
………1分
∴Sn+1=![]() Sn+2,即Sn+1-4=
Sn+2,即Sn+1-4=![]() (Sn-4), ………………………2分
(Sn-4), ………………………2分
因为S1-4=-2,∴![]() 是等比数列 ………………………3分
是等比数列 ………………………3分
∴Sn-4=(-2) (![]() )n-1即Sn=4[1-(
)n-1即Sn=4[1-(![]() )n],从而求得an=(
)n],从而求得an=(![]() )n-2 ………………5分
)n-2 ………………5分
(2)由![]() 得
得![]() 即
即![]()
化简得:![]() 即
即![]() ……7分
……7分
∵![]() ∴
∴![]()
∴![]() ………………………9分
………………………9分
∵an=(![]() )n-2 ,Sn=4[1-(
)n-2 ,Sn=4[1-(![]() )n] ∴
)n] ∴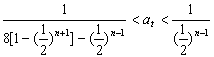
即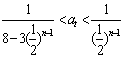 对
对![]() 都成立,则
都成立,则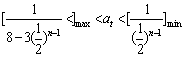 …10分
…10分
易得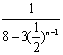 关于n递减,
关于n递减,![]() 关于n递增 ……………………11分
关于n递增 ……………………11分
∴n=1时它们分别取得最大与最小,从而有![]() 即
即![]()
∴t=3或4时成立。 ……………………12分
(3)不在。 ……………………13分
假设存在两项am,an的和在此数列中,设为第k项,即am+an=ak(m,n,k互不相等)
∵an=(![]() )n-2是关于n单调递减,∴不妨设k<m<n则有(
)n-2是关于n单调递减,∴不妨设k<m<n则有(![]() )m-2+(
)m-2+(![]() )n-2=(
)n-2=(![]() )k-2(*)
)k-2(*)
(*)式两边同乘以2n-2,则有![]() 显然这是不可能成立的。………16分
显然这是不可能成立的。………16分

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案